







|
|
|
|
|
||
Рассмотрим основные определения, связанные с движением жидкости. Прежде всего останосимся на понятии жидкость. Различают капельную жидкость (жидкость в широко принятом смысле) и газ; родовое понятие этих двух состояний называют жидкостью.
Способность жидкости изменять свою плотность под действием давления называют сжимаемостью. Во многих случаях сжимаемостью можно пренебречь, так как она незначительно влияет на конечный результат. Научная дисциплина, изучающая свойства несжимаемой жидкости, называется гидродинамикой или гидравликой, а свойства сжимаемых жидкостей изучает аэродинамика.
При скоростях движения, соизмеримых со скоростью звука, сжимаемость воздуха влияет на процесс движения жидкости; с ней связан выбор аэродинамических форм крыла и самолета в целом. На самолетах стали появляться стреловидные крылья, профили крыла стали тонкими и так далее. Сверхзвуковыми задачами занимаются также артиллеристы. Скорости полета пуль и снарядов (свыше 4000 км/ч) намного превышают скорость звука (1200 км/ч). Аэродинамика больших скоростей носит название газодинамики. Раздел физики, в котором изучают закономерности движения сжимаемых и несжимаемых жидкостей, называют механикой сплошных сред. Эта наука рассматривает не только жидкости, но и другие среды, например, сыпучие материалы или материальные среды, находящиеся не только в корпускулярном, но и в полевом состояниях.
В механике сплошных сред широко используется понятие струйки жидкости, то есть некоторой трубки траекторий, где скорости, направлены вдоль трубки, а поперек (через стенки трубки) жидкость не протекает. Опытами установлено, что течение жидкости при малых скоростях является ламинарным: слои жидкости скользят друг по другу не перемешиваясь. При высоких скоростях движение становится турбулентным, отдельные слои жидкости при таком течении перемешиваются за счет образования вихрей, скорость в каждой точке колеблется при этом около некоторого среднего значения. Существование ламинарного и турбулентного течений было установлено экспериментально английским физиком Рейнольдсом в 1883 году. На рис.1.1 представлен опыт Рейнольдса, в котором подкрашенная жидкость попадает из капилляра 1 в трубку 2, и ее движение принимает вид, характерный для ламинарного или турбулентного течения.
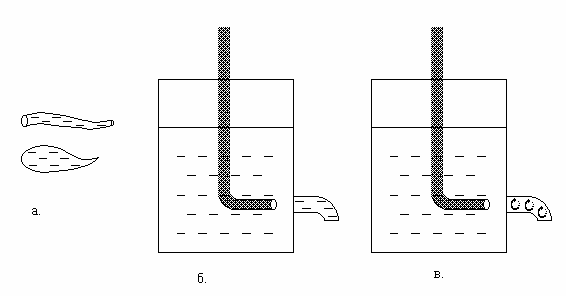
Установлено, что для круглых труб течение ламинарное, если безразмерный комплекс Vd/![]() < 2300 - число Рейнольдса,
< 2300 - число Рейнольдса, ![]() =
= ![]() /
/![]() (кинематическая вязкость),
(кинематическая вязкость), ![]() - динамическая вязкость,
- динамическая вязкость, ![]() - плотность жидкости, d - диаметр трубки.
- плотность жидкости, d - диаметр трубки.
Вязкость жидкости приводит к внутреннему трению. При течении жидкость сопротивляется деформации своих частей. Силы вязкости стараются затормозить быстро движущиеся части жидкости и ускорить медленные. Силы вязкости проявляются заметно там, где большая разность в скоростях движения отдельных частей жидкости, и именно вдоль поверхности обтекания.
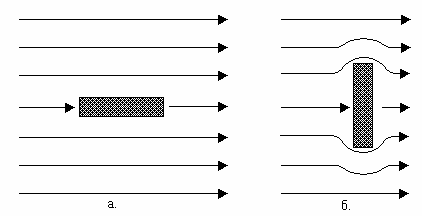
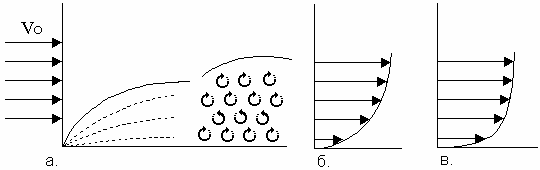
На рис.1.2 показан характер обтекания плоской пластины; в начальной ее части, как правило, наблюдается ламинарное течение, которое переходит в турбулентное. Тонкий слой жидкости, прилегающий к телу, в котором скорость меняется от нуля до скорости наблюдаемого потока, называется пограничным слоем. На рис.1.3 приведено распределение скоростей в ламинарном и турбулентном пограничных слоях.
Сила вязкости, отнесенная к величине поверхности S, носит название касательного напряжения ![]() =
=![]() / S, и пропорциональна градиенту скорости dV/dn; в направлении к нормали к поверхности, то есть
/ S, и пропорциональна градиенту скорости dV/dn; в направлении к нормали к поверхности, то есть ![]() ~ dV/dn;
~ dV/dn;
Если ввести коэффициент пропорциональности ![]() , то получим закон Ньютона: удельная сила трения пропорциональна удельному градиенту скорости
, то получим закон Ньютона: удельная сила трения пропорциональна удельному градиенту скорости
Параметр ![]() - коэффициент внутренней, или динамической вязкости, или просто вязкость жидкости.
- коэффициент внутренней, или динамической вязкости, или просто вязкость жидкости.
При dV/d![]() = 1 удельная сила вязкости
= 1 удельная сила вязкости ![]() =
= ![]() , то есть это сила трения на единицу поверхности соприкасающихся слоев жидкости при условии, что скорость на единице длины нормально к поверхности меняется на единицу. В системе CGS (г, см, с) единица измерения [
, то есть это сила трения на единицу поверхности соприкасающихся слоев жидкости при условии, что скорость на единице длины нормально к поверхности меняется на единицу. В системе CGS (г, см, с) единица измерения [![]() ] = г/(см*с) = пуаз (p); в технической системе единицы измерения силы Ньютоны (Н = кг*м/с2), а сила трения соответственно кг*м/(с2*м2) =
] = г/(см*с) = пуаз (p); в технической системе единицы измерения силы Ньютоны (Н = кг*м/с2), а сила трения соответственно кг*м/(с2*м2) = ![]() *м/см.
*м/см.
В дальнейшем вместо параметра ![]() будем также использовать понятие коэффициента кинематической вязкости
будем также использовать понятие коэффициента кинематической вязкости ![]() , равной отношению коэффициента вязкости
, равной отношению коэффициента вязкости ![]() к плотности
к плотности ![]() :
: ![]() =
= ![]() /
/![]() м2/с.
м2/с.
При решении многих задач гидродинамики можно изучать только изменение параметров на входе и выходе системы и обмен энергией в форме тепла и работы между системой и окружающей средой. При этом механизм процессов и значения параметров внутри системы не рассматриваются. Такой метод носит название балансового, или интегрального подхода и связан с составлением балансовых уравнений переноса энергии, массы и импульса.
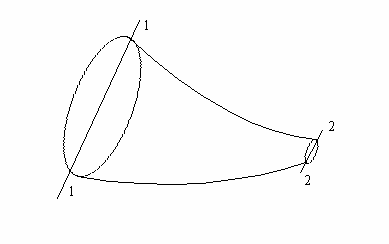
Рассмотрим процессы переноса массы в некотором объеме (трубке), представленном на рис.1.4. Сформулируем закон сохранения массы: за 1 с в сечение 1-1 входит ![]() 1V1S1 кг, а выходит
1V1S1 кг, а выходит ![]() 2V2S2 кг; изменение массы во времени обозначим dm/d
2V2S2 кг; изменение массы во времени обозначим dm/d![]() .
.
Введем среднюю скорость
Возможно, что внутри рассматриваемой трубки имеется источник или сток массы (продукты химических реакций и т.д.), и при этом производится Ri i-го химического вещества, тогда закон сохранения массы примет вид
Пример 1.1
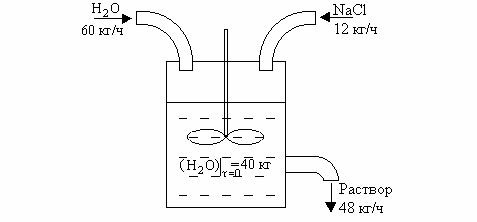
В перемешиваемую емкость подается вода с расходом 60 кг/ч и поваренная соль 12 кг/ч (рис.1.5). Раствор вытекает со скоростью 48 кг/ч; из-за перемешивания концентрации выравнены; в начале в баке было 40 кг H2O. Вычислить концентрацию XА (массовую долю соли) выходящего раствора через один час.
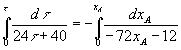
Напомним первый закон термодинамики для потока жидкости. Для этого введем следующие обозначения:
Q - количество подводимого тепла на 1 кг жидкости;
W - все виды работ, совершенных жидкостью над окружающей средой. Тогда подводимое к жидкости тепло идет на увеличение ее внутренней энергии ![]() E и на внешнюю работу W, то есть
E и на внешнюю работу W, то есть
Внутренняя энергия E состоит из кинетической Eк и потенциальной Eп: E = Eк + Eп. Потенциальная энергия - это запасенная работа, она состоит из энергии давления Eпp, энергии веса Eпg и внутренней (тепловой) энергии Eпt
Рассмотрим отдельные составляющие для сечения трубы 1-1, в которую входит за 1 сm кг.
Энергия сил давления - работа сил давления, расходующаяся на проталкивание массы газа через 1-1. Давление на воображаемый поршень p1S1, путь за 1 с равен u1, работа - p1S1u. Умножим и разделим это выражение на ![]() 1
1
Энергия веса газа равна работе силы веса mg при опускании центра тяжести сечения 1-1 на z1, отсчитываемому по вертикали от нивелира 0-0
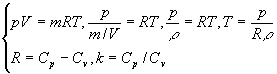 (1.9)
(1.9) 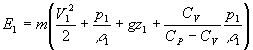 =
= 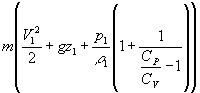 =
= 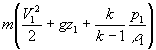 (1.10)
(1.10)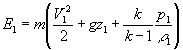 (1.11)
(1.11) 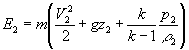 . (1.12)
. (1.12) Если на основании закона сохранения энергии приравнять выражения (1.10) и (1.11) для E1 и E2, то
Некоторые упрощения формул: V2/2 + i +gz = const.
Для горизонтальной трубы ![]() z = 0:
z = 0:
V2/2 + i = const.
Для воздуха k= 1.4 и из (1.9) и (1.10) получаем V2/2 + 3.5*p/![]() = const.
= const.
Для несжимаемой жидкости при выводе уравнения Бернулли мы должны бы учесть только Eк = mV2/2, потенциальную энергию давления Eпp = mp/![]() и потенциальную энергию веса Eпg = mgz. Внутренняя энергия газа для несжимаемой и невязкой жидкости (в условиях отсутствия отвода и подвода тепла) не может изменяться: из-за неспособности к сжатию и расширению несжимаемая жидкость не может изменить содержащееся в ней тепло. Если есть вязкое трение, то происходит выделение тепла и изменение температуры и у несжимаемой жидкости, но это мало влияет на плотность, и им можно пренебречь. Тогда
и потенциальную энергию веса Eпg = mgz. Внутренняя энергия газа для несжимаемой и невязкой жидкости (в условиях отсутствия отвода и подвода тепла) не может изменяться: из-за неспособности к сжатию и расширению несжимаемая жидкость не может изменить содержащееся в ней тепло. Если есть вязкое трение, то происходит выделение тепла и изменение температуры и у несжимаемой жидкости, но это мало влияет на плотность, и им можно пренебречь. Тогда
При действии разности давлений возникает движение, которому приходится преодолевать силы вязкости. Итак, силы инерции при движении жидкости уравновешиваются силами давления и вязкости.
Напомним, что критерий Рейнольдса: есть отношение сил инерции к силам вязкости. Рассмотрим шар l = 5 см, движущийся со скоростью V = 1 м/с в воде (Re = 50000), то есть силы инерции относятся к силам вязкости как 50000 к 1. Но игнорировать эти силы вязкости нельзя, так как получится, что шар, двигаясь в воде, не испытывает сопротивления. Давайте посмотрим в чем дело.
В примере а) сопротивление трения больше сопротивления давлению, б) сопротивление давления больше сопротивления трения. В общем случае одного порядка, однако, одно из них больше определяется формой тела, другое - площадью поверхности.
Ньютон выдвинул следующую гипотезу: на сопротивление влияют только те явления, которые происходят с передней стороны тела, но не с боков и сзади. То есть форма тела (при неизменной площади проекции S) и площадь его поверхности игнорировал. Далее он полагал, что частицы не взаимодействуют друг с другом и при встрече с телом приобретают импульс. Пусть плотность среды ![]() , проекция перпендикулярная движению S, скорость V, тогда масса жидкости, с которой приходит в соприкосновение за 1 с тело
, проекция перпендикулярная движению S, скорость V, тогда масса жидкости, с которой приходит в соприкосновение за 1 с тело ![]() SV. Этой массе сообщается скорость, пропорциональная скорости движения тела kV, тогда сопротивление тела равно импульсу в 1 с
SV. Этой массе сообщается скорость, пропорциональная скорости движения тела kV, тогда сопротивление тела равно импульсу в 1 с
Запишем (1.15) для горизонтальной трубы (z1 = 0)
Внесем в эту формулу поправку на сопротивление жидкости, то есть на падение давления ![]() p, вызванное сопротивлением
p, вызванное сопротивлением ![]() p = F/S, и, согласно (1.15),
p = F/S, и, согласно (1.15), ![]() p = k
p = k ![]() V2. Коэффициент k выберем так, чтобы падение давления выражалось в долях
V2. Коэффициент k выберем так, чтобы падение давления выражалось в долях ![]() V2/2. Договоримся писать
V2/2. Договоримся писать
Падение давления ![]() p, вызванное сопротивлением жидкости, в литературе иногда называют сопротивлением.
p, вызванное сопротивлением жидкости, в литературе иногда называют сопротивлением.
Рассмотрим тракт движения жидкости по каналу, где существуют сужения и расширения (рис 1.6). В этих местах происходит падение давления, которое обозначим ![]() pn, n+1, где n и n+1 номера мест сужения и расширения.
pn, n+1, где n и n+1 номера мест сужения и расширения.
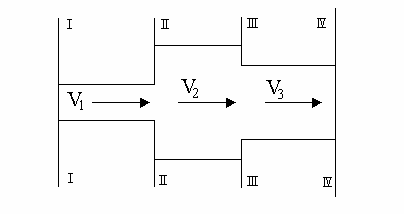
Тогда уравнение (1.15) для тонкого канала можно записать в виде
Уравнение (1.19) называют обобщенным уравнением Бернулли. Оно справедливо для реальных жидкостей.
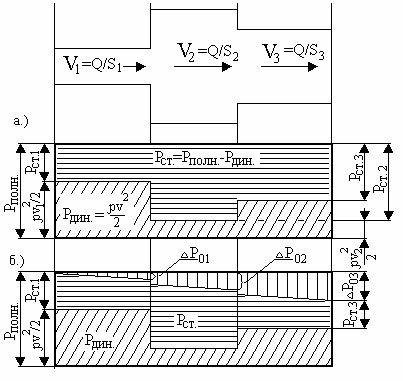
Рассмотрим эпюру давлений в каналах для идеальной (нет потерь) и реальной жидкостей (рис. 1.7). Эпюра построена для случая zn = 0 по уравнению (1.19). Для идеальной жидкости нет потерь, то есть ![]() pn, n+1 = 0, а для реальной жидкости на нижней части эпюры учтены потери из-за
pn, n+1 = 0, а для реальной жидкости на нижней части эпюры учтены потери из-за ![]() p
p ![]() 0.
0.
На основании теоремы количества движения определим местное гидравлическое сопротивление в местах изменения сечения канала. Иллюстрацию этой теоремы покажем на примере расчета давления при внезапном расширении канала. Заметем, что теорема количества движения позволяет определить движение жидкости в исходном и конечном состояниях, не касаясь механизма движения. Приведем общую формулировку теоремы: Изменение во времени количества движения (![]() mV) системы раздельных материальных потоков в жидкости равно сумме сил, действующих извне на систему, то есть
mV) системы раздельных материальных потоков в жидкости равно сумме сил, действующих извне на систему, то есть
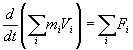 . (1.20)
. (1.20) Расширение канала. Рассмотрим внезапное расширение в сечении 2-2 и обратим внимание на то, что через цилиндрическую поверхность количество движения не переносится, то есть следует учитывать его изменение только по площадям S1 и S2. В этих сечениях количество движения равно (![]() SV1)V1 и (
SV1)V1 и (![]() SV2)V2, то есть изменение количества движения за одну секунду равно
SV2)V2, то есть изменение количества движения за одну секунду равно ![]() S2V22 -
S2V22 - ![]() S1V12; внешними силами являются силы давления F =pS. Тогда, уравнение (1.20) примет вид для сечения 2-2
S1V12; внешними силами являются силы давления F =pS. Тогда, уравнение (1.20) примет вид для сечения 2-2
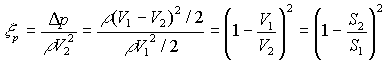 . (1. ..)
. (1. ..) Разветвление струи из одного общего канала (например, канала после вентилятора электрической машины) в несколько каналов (например, в зазор электрической машины и в камеру соседних каналов рис.1.8) можно рассматривать по той же схеме как внезапное расширение канала и вычислять гидравлическое сопротивление для этого случая по формуле
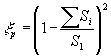 . (1. ..)
. (1. ..) 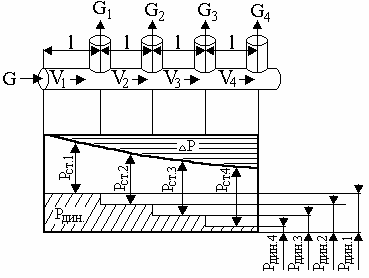
Сужение канала (рис 1.10,а). Гидравлическое сопротивление в этом случае вычисляется по формуле
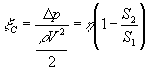 . (1. ..)
. (1. ..) 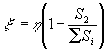 ,(1. ..)
,(1. ..) 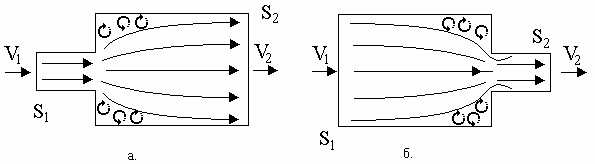
Движение струи через отверстие в стенке (рис. 1.10 б). Из-за искривления линий тока полезно используется лишь часть сечения отверстия. Обозначим через ![]() отношение площади сечения узкого сечения потока в отверстии S0 к площади отверстия и назовем его коэффициентом заполнения сечения.
отношение площади сечения узкого сечения потока в отверстии S0 к площади отверстия и назовем его коэффициентом заполнения сечения.
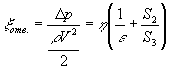 .(1. ..)
.(1. ..) 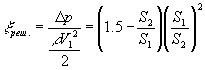 .(1. ..)
.(1. ..) Диффузор (расширенный канал). Резко возрастает интенсивность турбулизации потока по сравнению с каналом неизменного сечения.
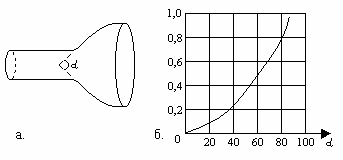
Сопротивление диффузора зависит от угла ![]() (угол раскрытия). Надо учитывать сопротивление трения
(угол раскрытия). Надо учитывать сопротивление трения
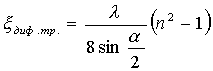 .(1. ..)
.(1. ..) 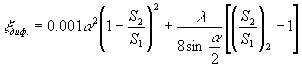 .(1. ..)
.(1. ..) Коэффициент сопротивления при повороте струи определяется из графика рис.11; для угла 90 °
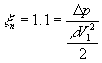 .(1. ..)
.(1. ..) Ответвление доли потока или нескольких долей потока. Потери состоят из внезапного расширения в месте разделения потока плюс потери на поворот в боковом ответвлении. Скорость до ответвления W, а после - V.
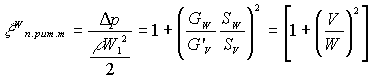 .
. 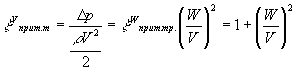 .
. Потери выт. тр. составляют потери на турбулентное смешение потоков с разными скоростями плюс потери на поворот потока при выходе из бокового отверстия.
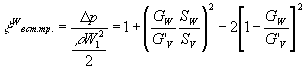 =
= 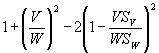 .
. 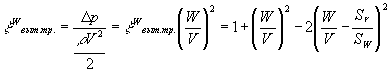 .
. Двигаясь в канале, струя жидкости или газа преодолевает сопротивления разного вида. Условно эти сопротивления можно считать последовательно соединенными между собой, например, при повороте канала одновременно имеется и трение о стенки. По аналогии с электрической цепью аэродинамический и гидравлический тракты принято изображать в виде сопротивлений, соединенных между собой отрезками без сопротивлений (рис.13).
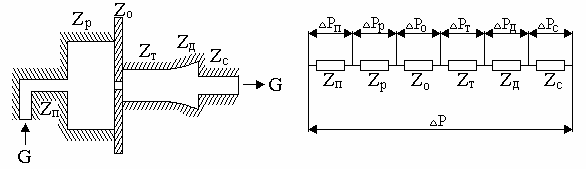
Потери давления ![]() p на преодоление какого-нибудь гидравлического сопротивления принято вычислять с помощью коэффициента местного сопротивления
p на преодоление какого-нибудь гидравлического сопротивления принято вычислять с помощью коэффициента местного сопротивления ![]() . Чтобы исключить из расчета переменную величину скорости движения, удобно выразить
. Чтобы исключить из расчета переменную величину скорости движения, удобно выразить ![]() p как функцию G, так как он постоянен.(1.18)
p как функцию G, так как он постоянен.(1.18)
Здесь z - коэффициент гидродинамического (аэродинамического) сопротивления, соответствующий ![]() коэффициенту местного сопротивления данного вида. Например,
коэффициенту местного сопротивления данного вида. Например,
Сопротивление внезапного расширения каналов (формула дана для динамического давления в широком сечении)
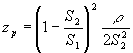 .(1. ..)
.(1. ..) 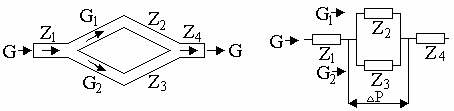
При разветвлении струи из-за нелинейности закона Аткинсона расчеты усложняются. Так как p давление в каком-либо данном сечении общего канала может иметь только одно значение, то ![]() p разность давлений на параллельных участках постоянная:
p разность давлений на параллельных участках постоянная:
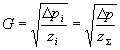 .
. 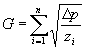 .(1. ..)
.(1. ..) 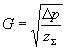 .(1. ..)
.(1. ..)