Предыдущий уровень изложения текущего раздела   Текущий уровень изложения предыдущего раздела   Текущий уровень изложения следующего раздела   Следующий уровень изложения текущего раздела   Уровень:


Дифференциальное уравнение переноса массы

2.1 Молекулярный и конвективный перенос массы

Прежде чем переходить к общему закону сохранения массы, приведем частные закономерности переноса массы.
Закон Фика. В 1855 году немецкий физик Адольф Фик сформулировал следующий закон молекулярного переноса массы:

,(2.1)
где j - поток массы, то есть переносимое через нормальную единичную площадку количество массы за 1 с; - плотность переносимой массы кг/м3, n - нормаль к единичной площадке; D - коэффициент диффузии.

В принятой системе единиц эти величины имеют следующие единицы измерения:

[j] = кг/(м2c), [ ] = кг/м3, [n] = м, [D] = м2/с.

Если концентрация вещества измеряется не в кг/м3, а в других единицах, например, относительная концентрация м3/м3=%, объемная м3, то единицы измерения коэффициента диффузии будут иные.

Коэффициент диффузии меняется в очень широких пределах: на десять порядков, от 10-4 до 10-14 м2/с.

Если помимо молекулярного переноса массы существует и конвективный, то общий поток массы описывается обобщенным законом Фика

,(2.2)
где Vx - составляющая скорости в направлении оси x, если ось x и направление нормали совпадают, то n = x.

Рассмотрим перенос массы в движущейся среде.

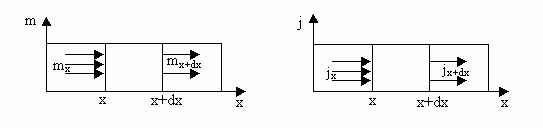
2.2 Вывод дифференциального уравнения



Пусть в направлении x через тело переносится количество массы mx, на расстояние (x + x) через площадку S = 1 м2 проходит уже иное количество массы , это происходит за счет изменения количества массы m в объеме x (рис. 2.1,a). Запишем закон сохранения массы: разница между входящей в объем массой mx и выходящей из него идет на изменение количества dm количества массы в объеме x, то есть

mx = + dm(2.3)

Запишем количество массы mx и , переносимое через единичную площадку за время d через потоки jx и :

mx = jxd , = d ,
а изменение количества в объеме x = 1 через изменение плотности d
dm = ( / )dxd .
Тогда, подставляя эти значения масс в (2.3), получим
,
возьмем предел этого отношения при x 0
,
Закон сохранения массы примет вид
,(2.4)
Подставим в (2.4) вместо j обобщенный закон Фика (2.2)
,(2.5)

Для трехмерной задачи следует записать это выражение по направлениям осей y и z, после сложения этих выражений получаем дифференциальное уравнение сохранения массы в дифференциальной форме

(2.6)

Здесь приняты следующие обозначения векторного анализа:
Полная производная функции f

(2.7)
Градиент функции f
(2.8)
Дивергенция функции f
(2.9)

Рассмотрим частные случаи уравнения (2.6):
Несжимаемая жидкость. По определению для несжимаемой жидкости = const, что приводит из (2.6) к следующему определению несжимаемой жидкости:

(2.10)
тогда уравнение (2.6) примет вид
(2.11)
Если коэффициент диффузии величина постоянная, то есть D = const, и
,
Здесь принята во внимание следующая формула из векторного анализа
,(2.12)
где символ носит название оператора Лапласа.
Если нет молекулярного переноса, то есть D = 0, то уравнение (2.6) примет вид
(2.13)
и носит название уравнения сплошности.