







|
|
|
|
|
||
1.4 Примеры
Решение.
Используя универсальную тригонометрическую подстановку, имеем  . Из равенства
. Из равенства ![]() получим
получим ![]() , откуда
, откуда  . Подставим эти выражения в данный интеграл:
. Подставим эти выражения в данный интеграл: 
Последний переход сделан по формуле ?7.14 .
Решение.
Очевидно, подынтегральная функция удовлетворяет условию(1) , поэтому используем подстановку ![]() . При этом
. При этом ![]() . Тогда
. Тогда  =
= =
=
Решение.
Сначала преобразуем интеграл к более удобному виду:  .
.
Теперь сделаем замену переменной ![]() . Тогда
. Тогда  и
и 
Решение.
Внесем ![]() под знак дифференциала:
под знак дифференциала: ![]() . Тогда
. Тогда
![]() =
=
Решение.
Воспользуемся формулой понижения степени ?7.7 :

Решение.
Сначала, с помощью формулы ?7.5 преобразуем подынтегральную функцию: 
Теперь сделаем замену переменной ![]() . При этом
. При этом  и
и  . Возвращаясь к нашему интегралу, получим
. Возвращаясь к нашему интегралу, получим 
Решение.
В числителе подынтегральной функции стоит единица, которую запишем как ![]() . Тогда
. Тогда 


При вычислениями мы воспользовались формулами 1 и 8 .
Решение.
![]() =
=
 .
.
Решение.
![]() =
= .
.
Пример10. Найти интеграл  .
.
Решение.
Вычислим этот интеграл с помощью универсальной тригонометрической подстановки  . Тогда,
. Тогда,  и
и  , следовательно,
, следовательно,  =
=
 .
.
Пример11. Найти интеграл  .
.
Решение.
Вычислим этот интеграл с помощью универсальной тригонометрической подстановки  . Тогда,
. Тогда,  ,
,  и
и  , следовательно,
, следовательно,
 =
= .
.
Пример 12. Найти интеграл  .
.
Решение.
Подынтегральная функция ? это рациональная функция, удовлетворяющая условию ![]() . Используя подстановку
. Используя подстановку ![]()
![]() , получаем
, получаем
![]() .
.
Пример 13. Найти интеграл  .
.
Решение.
Подынтегральная функция ? это рациональная функция от ![]() и
и ![]() , удовлетворяющая условию
, удовлетворяющая условию ![]() . Поэтому, применяем подстановку
. Поэтому, применяем подстановку ![]() .СМ * Сначала преобразуем подынтегральную функцию следующим образом
.СМ * Сначала преобразуем подынтегральную функцию следующим образом  .Тогда,
.Тогда,  и
и  =
= .
.
Пример 14. Найти интеграл  .
.
Решение.
Подынтегральная функция имеет вид ![]() где m и n - целые числа и n = 5, то есть нечетное положительное число см п4. Внесем
где m и n - целые числа и n = 5, то есть нечетное положительное число см п4. Внесем ![]() под знак дифференциала, а
под знак дифференциала, а ![]() выразим через
выразим через ![]() . Получим
. Получим

 .
.
Пример 15. Найти интеграл ![]() .
.
Решение.
Подынтегральная функция имеет вид ![]() , где m = 3, то есть нечетное положительное число. Сделаем замену переменной
, где m = 3, то есть нечетное положительное число. Сделаем замену переменной ![]() .Тогда
.Тогда  и
и ![]() =
= =
= .
.![]()
Пример 16. Найти интеграл ![]() .
.
Решение.
Подынтегральная функция имеет вид ![]() , где m = 2, n = 2. Используя формулы понижения степени ?7.5 и ?7.7 , получим
, где m = 2, n = 2. Используя формулы понижения степени ?7.5 и ?7.7 , получим  .
.
Таким образом ![]() =
= .
.
Пример 17. Найти интеграл ![]() .
.
Решение
. Подынтегральная функция имеет вид ![]() , где m = 0, n = 6. Используя формулу понижения степени ?7.8 , получим
, где m = 0, n = 6. Используя формулу понижения степени ?7.8 , получим ![]() =
=
 .
.
Пример 18. Найти интеграл  .
.
Решение.
Подынтегральная функция имеет вид ![]() , где m = 0, n = - 4. Используя подстановку
, где m = 0, n = - 4. Используя подстановку ![]() , получим
, получим  и
и  . Следовательно,
. Следовательно,  .
.
Пример 19. Найти интеграл  .
.
Решение.
Подынтегральная функция имеет вид ![]() . Делая подстановку
. Делая подстановку ![]() и используя формулы
и используя формулы  и
и  , получим
, получим 
 .
.
Пример 20. Найти интеграл ![]() .
.![]()
Решение.
Подынтегральная функция имеет вид ![]() , где m = 6. Используя формулу
, где m = 6. Используя формулу 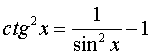 и заметим, что
и заметим, что  . Тогда
. Тогда

 .
.
Пример 21. Найти интеграл  .
.
Решение.
Подынтегральная функция имеет вид ![]() , где
, где ![]() ,
, ![]() Используем формулу
Используем формулу  и заметим, что
и заметим, что  . Тогда
. Тогда 

Пример 22. Найти интеграл  .
.
Решение.
Подынтегральная функция имеет вид ![]() Воспользуемся формулой ?7.11 :
Воспользуемся формулой ?7.11 : 
Пример 23. Найти интеграл  .
.
Решение.
Применим к произведению  формулу ?7.9
формулу ?7.9  Используя ту же формулу, получим:
Используя ту же формулу, получим: 
