Уровень: основной текст примеры упражнения указания решения

Замена переменной в неопределенном интеграле

Пусть требуется найти интеграл , где функция непрерывна на некотором интервале . Сделаем замену переменной в подынтегральном выражении, положив , где - функция непрерывно дифференцируемая на некотором интервале T и имеющая обратную функцию

(1)

определенную на . Так как , получим

(2)

то есть, вычисление исходного интеграла сводится к вычислению

интеграла , стоящего в правой части равенства (2.). По окончании вычислений необходимо вернуться к переменной , пользуясь равенством (1).

Замечание 1.

Часто целесообразно подобрать замену переменной не в виде , а в виде .

Рассмотрим два примера.

Пример 1. Найти интеграл .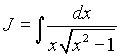

Решение. Положим

,

тогда 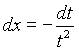. Следовательно,

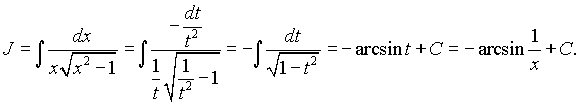
На последнем шаге использовано равенство , которое, очевидно, следует из равенства . Ответ: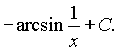

Пример 2. Найти интеграл .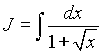

Решение. Положим

,

тогда . Следовательно, Перейдем в данном интеграле к переменной :

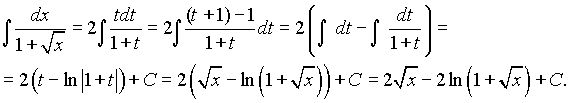
Ответ:

Замечание 2.

Обратите внимание, что в примере 1 замена переменной выбрана в виде , а в примере 2. замена переменной выбрана в виде .

Отметим, что не существует одного общего правила для выбора подстановки, позволяющей вычислять интегралы. Существуют частные правила для некоторых типов интегралов. Дадим некоторые рекомендации.

А) Если подынтегральная функция иррациональная, то подстановка выбирается так, чтобы замена переменной под знаком интеграла приводила к рациональной функции от новой переменной (см.примеры 1, 3, 4.

Б) Если подынтегральная функция есть дробно-рациональная функция от трансцендентной (например, от функции ), то выбирают замену, приводящую к алгебраической рациональной функции (см. .пример 2).

Замечание 3.

Иногда при вычислении интеграла методом замены переменной выбор подстановки можно осуществить различными способами. При этом могут получаться ответы, отличающиеся друг от друга формально (т.е., по виду). В частности, отличающиеся видом константы.

Рассмотрим такую ситуацию на примере 2.

В интеграле 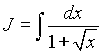сделаем замену переменной, полагая (в отличие от замены ). Тогда , значит , следовательно, . Переходим в данном интеграле к переменной t:

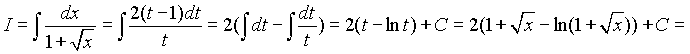
Таким образом,

Если сравним полученные результаты, то увидим, что слагаемые, зависящие от x совпадают, а произвольная константа в первом случае обозначенная через C, во втором случае имеет вид С+2 . Из определения неопределенного интеграла следует, что эти ответы идентичны.