|
|
|
|
|
|
||
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
Пусть в точках двусторонней поверхности 
задана непрерывная функция 
. Выберем на поверхности определенную сторону. Разобьем поверхность сетью произвольно проведенных кривых на части 
В пределах каждой части
выберем произвольно по точке 
, вычислим в ней значение данной функции. Это значение 
умножим на проекцию (
) части на плоскость Оху (а не на площадь , как это было в случае поверхностного интеграла первого типа). При этой числу , приписывается определенный знак, а именно:
если в точках нормаль, отвечающая выбранной стороне поверхности, составляет с осью Oz острый угол, то через обозначаем площадь проекции , взятую со знаком УплюсФ; если же упомянутая нормаль составляет с осью Оz тупой угол, то под будем понимать площадь этой проекции, взятую со знаком УминусФ. Составим сумму всех таких произведений:
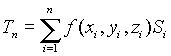(4.22)
Поверхностным интегралом второго типа называется предел суммы (4.22) при
:
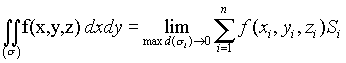(4.23)
Где 
- диаметр .
Аналогично определяются интегралы
, 
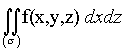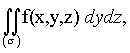(4.24)
причем для выбора знака проекции элемента служит угол между нормалью, отвечающей выбранной стороне поверхности, и осью Оу или Ox.
Наиболее общим видом поверхностного интеграла второго типа служит интеграл
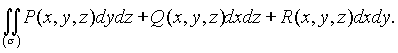(4.25)
где 
, 
, 
- функции от 
определенные и непрерывные в точках двусторонней поверхности .
Поверхностный интеграл второго типа обладает всеми свойствами поверхностного интеграла первого типа. за исключением одного: при изменении стороны поверхности интеграл (4.25) меняет знак.
Поверхностные интегралы второго типа дующим образом. Если поверхность
однозначно проектируется в область 
плоскости Оху и 
ее уравнение, то
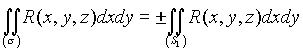, (4.26)
где знак + берется в том случае, если на выбранной стороне поверхности 
, и знак минус - если 
. Аналогично, если однозначно проектируется в область 
или 
на плоскости Oxz или Oyz, т. е. может быть задана уравнением 
или 
, то
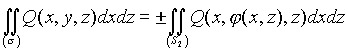(4.27)
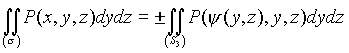(4.28)
где в случае (4.27) берется тот же знак, что и у 
, а в случае (4.28) Ч знак 
.
Для вычисления интеграла общего вида (4.25) используются те же формулы (4.26)Ч (4.27), если поверхность однозначно проектируется на все три плоскости. В более сложных случаях разбивается на части, обладающими указанными свойствами, а интеграл (4.25) - на сумму интегралов по этим частям. Поверхностные интегралы обоих типов связаны формулой
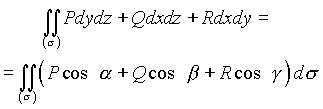(4.29)
где 
- направляющие косинусы нормали, направленной в ту сторону поверхности, по которой берется интеграл.
Приведенные теоретические положения используются при рассмотрении
примеров и решении упражнений.