Поверхностные интегралы I рода. Примеры. Упражнения
Задача 19. Решение:
Используем формулу (4.19):
 .
.
1) Поверхность 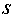 представляет собой часть конуса
представляет собой часть конуса 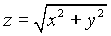 .
.
2) Для функции 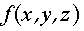 имеем:
имеем: 
3) Область 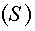 представляет собой плоское множество:
представляет собой плоское множество: 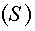 =
=
4) Для  имеем:
имеем:  =
= =
= .
.
5) Окончательно, из (4.19) получаем: 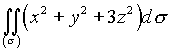 =
= =
=
Задача 20. Решение:
Используем формулу (4.19):
 .
.
1) Поверхность 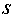 представляет собой верхнюю часть (
представляет собой верхнюю часть ( ) цилиндра радиуса 3 с образующими параллельными оси
) цилиндра радиуса 3 с образующими параллельными оси  и ограниченную плоскостями z=0, z=1.
и ограниченную плоскостями z=0, z=1.
2) Для функции 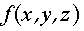 имеем:
имеем: 
3) Область 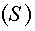 представляет собой плоское множество:
представляет собой плоское множество: 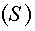 =
=
4) Для  имеем:
имеем: 
5) Окончательно, из (4.19) получаем: 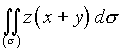 =
=
Ответ 36.
Задача 21.Решение: Используем формулу
 .
.
- Поверхность
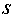 представляет собой часть конуса
представляет собой часть конуса 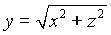 вырезанная цилиндром
вырезанная цилиндром  единичного радиуса.
единичного радиуса. - Для функции
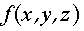 имеем:
имеем: 
- Область
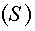 представляет собой плоское множество:
представляет собой плоское множество: 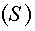 =
=
- Для
 имеем:
имеем:  =
= =
=
- Окончательно, получаем:
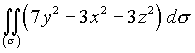 =
=
Задача 22. Решение: Используем формулу
 .
.
- Поверхность
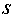 представляет собой часть кругового параболоида
представляет собой часть кругового параболоида 
- Для функции
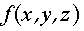 имеем:
имеем: 
- Область
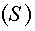 представляет собой плоское множество ? окружность единичного радиуса с центром в начале координат.
представляет собой плоское множество ? окружность единичного радиуса с центром в начале координат. - Для
 имеем:
имеем:  =
= =
=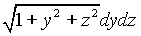
- Окончательно, получаем
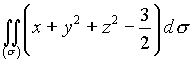 =
=
Задача 23. Решение: Используем формулу (4.19):
 .
.
- Поверхность
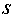 представляет собой часть гиперболического параболоида
представляет собой часть гиперболического параболоида 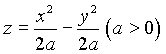 , вырезаемую цилиндром с образующими параллельными оси Oz.
, вырезаемую цилиндром с образующими параллельными оси Oz.
- Для функции
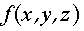 имеем:
имеем: 
- Область
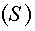 представляет собой плоское множество выделенное линией с уравнением
представляет собой плоское множество выделенное линией с уравнением 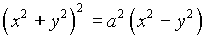
- Для
 имеем:
имеем:  =
= =
=
- Окончательно, из (4.19) получаем, переходя к полярным координатам:
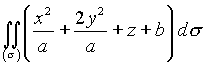 =
=









 .
. =
=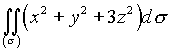 =
= =
=
 .
.![]() представляет собой верхнюю часть (
представляет собой верхнюю часть (![]() ) цилиндра радиуса 3 с образующими параллельными оси
) цилиндра радиуса 3 с образующими параллельными оси ![]() и ограниченную плоскостями z=0, z=1.
и ограниченную плоскостями z=0, z=1. 
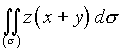 =
=
 .
. =
=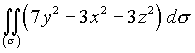 =
=
 .
.

 =
=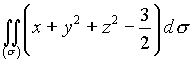 =
=
 .
.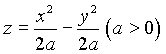 , вырезаемую цилиндром с образующими параллельными оси Oz.
, вырезаемую цилиндром с образующими параллельными оси Oz.
 =
=
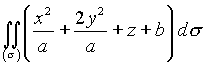 =
=