Предыдущий уровень изложения текущего раздела   Текущий уровень изложения предыдущего раздела   Текущий уровень изложения следующего раздела   Следующий уровень изложения текущего раздела   Уровень:


Вычисление площади сектора, ограниченного кривой, заданной в полярных координатах

2.6.1.c Примеры.

 1. Вычислить площадь, ограниченную одним лепестком лемнискаты Бернулли .

Решение.

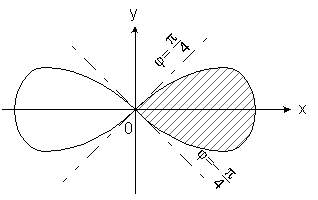
Подставляем уравнение кривой в формулу (1) п.2.6.1.с и, учитывая, что кривая расположена в секторе от = - /4

до = /4 , получим .

Можно было, используя симметрию кривой, интегрировать по промежутку и полученный результат удвоить.



2. Вычислить площадь фигуры, лежащей между кривыми r = 2 - cos и r = cos

Решение.

Используя симметрию кривой, вычислим площадь фигуры, расположенной в верхней части плоскости. Найдем сначала площадь, ограниченную линией

r = 2 ? cos и осью ОХ: .

Вторая кривая r = cos является окружностью радиуса 1/2. Поэтому площадь внутри круга можно вычислить по формуле . Искомая площадь равна удвоенной разности вычисленных площадей: .



3. Вычислить площадь между кривыми x2+y2=2x, x2+y2=6x, и .

Решение.

Перейдем к полярным координатам по формулам x = r cos , y = r sin . Подставляя эти формулы в уравнения данных линий, получим их уравнения в полярных координатах: , , и . Таким образом нам надо вычислить площадь фигуры, ограниченной дугами двух окружностей и двумя лучами. Будем искать эту площадь как разность двух секторов, лежащих между этими лучами: .