Координатный способ задания движения точки

Пример. Движение точки в плоскости Oxy задано уравнениями (x,y - в метрах; t - в секундах):

x = 3t; y = 2t².

Решение. Для определения траектории исключаем из уравнений движения время t и находим уравнение траектории в виде, дающем зависимость между координатами x и y движущейся точки.

Из первого уравнения находим t = x / 3 и, подставляя это выражение для t во второе уравнение, получаем y = 2x² / 9. Следовательно, траекторией точки является парабола с вершиной в начале координат О.

В заданный момент времени t₁ = 1(c) точка имеет координаты x₁ = x(t₁) = 3 (м), y₁ = y(t₁) = 2 (м).

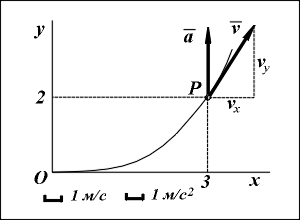
Определяем проекции и модуль скорости точки в момент времени t₁ = 1(c):

v_x = = (3t)^· = 3;

v_y = = (2t²)^· = 4t; v_y(t₁) = 4 (м/с);

v(t₁) =( v_x² + v_y² ) = ( 3² + 4² ) = 5 (м/с).

Определяем проекции и модуль ускорения точки в момент времени t₁ = 1(c):

a_x = _x = (3)^· = 0;

a_y = _y = (4t)^· = 4;

a(t₁) =( a_x² + a_y² ) = | a_y | = 4 (м/с²).