







|
|
|
|
|
||
Отношение ежегодного прироста численности dX некоторой популяции к ее общей численности Х назовем коэффициентом прироста популяции r. При постоянном значении этой величины в течение всего периода времени закон роста является линейным и приводит к экспоненциальной зависимости
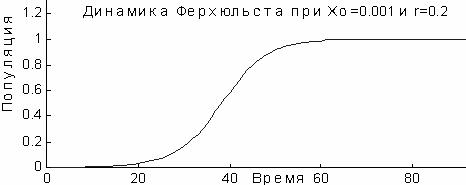
При коэффициенте r = 5% = 0,05, популяция удваивает свою численность каждые 14 лет. Однако для роста всегда существуют пределы и зависимость (1) справедлива на ограниченных промежутках времени. Ограничения на рост сформулировал в 1845 г. П. Ф. Ферхюльст: любая экологическая ниша способна обеспечить существование популяции только определенного размера Х, и коэффициент прироста должен снижаться при приближении размера популяции к Х. Иными словами, переменный коэффициент r делал процесс нелинейным. Прошло свыше ста лет прежде чем осознали вытекающие из этого необычные следствия. В частности, когда параметры роста превысят 200% . При малой величине популяции ее рост приводит к повышению оптимального размера, это вызывает ответную реакцию, и популяция уменьшается до значений меньших Х, затем появляются устойчивые колебания между большим и малым размером.
Когда параметр роста превысит 245% , колебания все более усложняются, процесс приходит к устойчивым периодическим колебаниям и далее к хаосу . Это значит, что система выходит из-под контроля, и нельзя предсказать ее поведение на длительное время. Следовательно, динамика Ферхюльста позволяет найти сценарий, по которому порядок превращается в хаос. Эта проблема требует более последовательного изучения модели роста популяции.
Воспользуемся методом анализа, рассмотренным paнee и построим модель роста какой-либо популяции [15].
Пусть х0 - начальная численность популяции, а хn - ее численность через n лет. Коэффициент прироста R, по определению, есть относительное изменение численности за 1 год
Допустим, что R = r - константа, и сформулируем вытекающий из (2) закон динамики роста
Через n лет численность популяции будет равна
Как указывалось выше, для ограничения этой численности (экспоненциальный рост) Ферхюльст заставил меняться коэффициент прироста r и быть пропорциональным (1 - xn), т. е. допустил, что
При хn<1 происходит рост популяции, а при хn=1 - рост прекращается. Из (3) и (4) следует закон, управляющий динамикой процесса
Для х0 = 0 и х0 = 1 роста популяции нет. Действительно, при х0 = 0 популяция попросту отсутствует, а при х0 = 1 из (5) следует х1=(1+r)-r= 1, т. е. тоже нет роста. Однако, если начальная численность хоть немного будет отличаться от нуля, 0<х0<1, то при r>0 через год численность х1 возрастет: х1 > х0 + rх0. Последующие значения х1, х2, ... растут пока не достигнут единицы.
Проследим, как изменяются малые отклонения ![]() n=хn-1; для этого линеаризуем (5)
n=хn-1; для этого линеаризуем (5)
Обозначим ![]() n=1=хn+1-1 и линеаризуем последнее выражение
n=1=хn+1-1 и линеаризуем последнее выражение
Видно, что при 0<r<2 по абсолютной величине ![]() n+1 меньше, чем
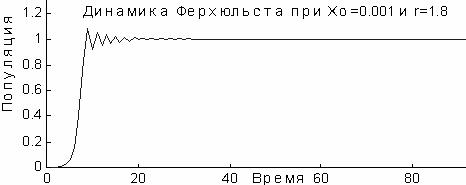
n+1 меньше, чем ![]() n. Выше был приведен график изменения во времени популяциидля случая r = 1,8 и начального значения х0 = 0,001. Величина х поначалу растет, т. к. она менее 1, но на третьем шаге ее значение несколько превышает х0 = 0,1, затем убывает в соответствии с (6):
n. Выше был приведен график изменения во времени популяциидля случая r = 1,8 и начального значения х0 = 0,001. Величина х поначалу растет, т. к. она менее 1, но на третьем шаге ее значение несколько превышает х0 = 0,1, затем убывает в соответствии с (6): ![]() n+1= -0.8
n+1= -0.8![]() n, и процесс приближается к конечному состоянию х = 1.
n, и процесс приближается к конечному состоянию х = 1.
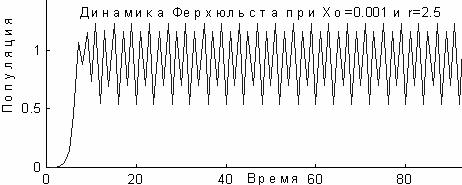
Однако при r> 2 соотношение (6) предсказывает рост отклонений ![]() n, и состояние равновесия х = 1 уже неустойчиво. Из графика видно, что процесс при r = 2,5 начинает периодически осциллировать между двумя уровнями.
n, и состояние равновесия х = 1 уже неустойчиво. Из графика видно, что процесс при r = 2,5 начинает периодически осциллировать между двумя уровнями.
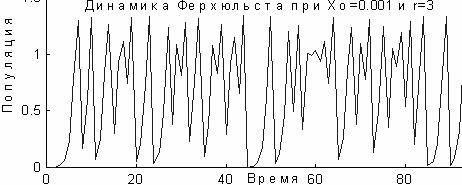
С ростом r анализ соотношения (5) дает следующий результат: для r = 2,5 получается ломанная линия, т. е. процесс переходит к устойчивым периодическим колебаниям с периодом 4, при дальнейшем росте r происходит удвоение периодов колебаний. Наконец, при r =2,572 процесс вообще перестает быть периодическим, прыгает и, несмотря на изначальную детерминированность, его невозможно прогнозировать на большие периоды времени. Подобное поведение называют хаотическим, график построен для х0 = 0,001 и r=3.
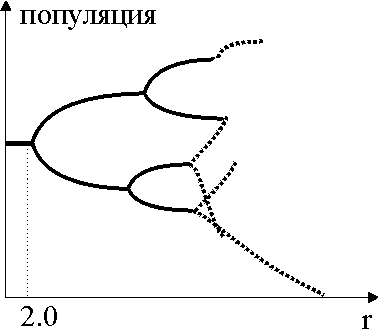
В случае процесса Ферхюльста все возможные типы поведения можно представить с помощью бифуркационной диаграммы, которая отражает зависимость динамики популяции от параметра r. В процессе вычислений находили особенности переходного периода и отмечали асимптотическое значение х, т. е. выходили на аттрактор. Он состоит из одной точки при r<2, из двух точек при 2<r<2,449, затем из 4, 8, 16, ... точек вплоть до хаоса, где точки аттрактора заполняют целые полосы.
При точном анализе точек бифуркации в процессе Ферхюльста в 1977 г. обнаружена замечательная закономерность. Она касается длин интервалов, при которых устойчивым является периодическое движение с некоторым определенным интервалом. Эти интервалы сокращаются при каждом удвоении периода, причем множитель, характеризующий сокращение
Это число называют "числом Фейгенбаума".
Это открытие вызвало большую активность ученых. Показано, что сценарий удвоения периода наблюдается и в турбулентном потоке жидкости, и в нелинейных колебаниях в электрических цепях, и в физиологии (переход от нормального цикла к фибрилляции).