







|
|
|
|
|
||
4.2. Основные понятия геометрической оптики4.2.1. Волновой фронт и лучиИз приближения коротких волн, рассмотренного в параграфе 4.1, следует подход к изучению распространения света на основе понятия лучей. Луч - это прямая или кривая линия, вдоль которой распространяется энергия светового поля. Таким образом, геометрическая оптика описывает распространение электромагнитного поля как распространение лучей в пространстве. Кроме лучей существует еще одно важное понятие геометрической оптики - волновой фронт. Волновой фронт - это поверхность равной фазы или равного эйконала:
Изменяя значение Основные свойства волновых фронтов:
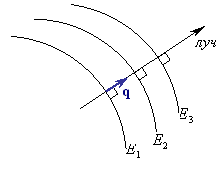 Рис.4.2.1. Волновые фронты и лучи. В геометрической оптике лучи определяются как нормали к волновому фронту. Направление луча совпадает с направлением распространения волнового фронта и определяется оптическим вектором* Уравнение волнового фронта:
Если среда, в которой распространяется свет однородна, то есть ее показатель преломления не зависит от пространственных координат Следовательно, в однородной среде лучи являются прямыми линиями. На границе раздела двух сред луч преломляется в соответствии с законом преломления. В неоднородной среде, где показатель преломления непостоянен, лучи искривляются в сторону градиента показателя преломления 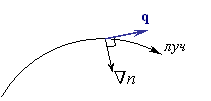 Рис.4.2.2. Оптический луч в неоднородной среде. С помощью изучения траекторий лучей в неоднородной среде можно анализировать влияние неоднородностей на распространение света. Например, при использовании наземных оптических телескопов - учитывать неоднородность атмосферы Земли. 4.2.2. Оптическая длина лучаПусть имеется однородная среда 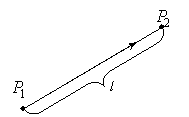 Рис.4.2.3. Оптическая длина луча в однородной среде. Оптическая длина луча в однородной среде: Оптическая длина луча в однородной среде - это произведение геометрической длины пути луча
Если среда является неоднородной 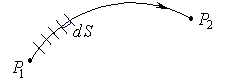 Рис.4.2.4. Оптическая длина луча в неоднородной среде. В этом случае оптическая длина луча вычисляется как криволинейный интеграл:
Если есть несколько однородных сред, разделенных границами (рис.4.2.5), то оптическая длина луча вычисляется как сумма оптических длин луча в каждой среде:
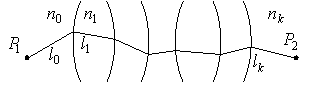 Рис.4.2.5. Оптическая длина луча в нескольких средах. Если среды неоднородные, то можно пользоваться выражением (4.2.5), считая интеграл по ломаной линии. 4.2.3. Конгруэнция лучей.Пучок лучей - это множество линий, пронизывающих пространство. Но не каждое множество кривых или прямых линий, пронизывающих пространство, можно назвать пучком лучей. Для того чтобы множество линий образовывало пучок лучей, нужно чтобы это множество составило конгруэнцию. Конгруэнция - это такая совокупность линий в пространстве, для которой выполняется условие, что через любую точку пространства можно провести только одну линию из этой системы (рис.4.2.6). 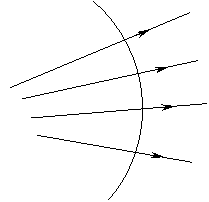 Рис.4.2.6. Конгруэнция. Конгруэнция определяется следующим уравнением:
где запись Нормальная конгруэнция - это конгруэнция, все линии которой пересекаются некоторой поверхностью под прямым углом. Пучок лучей - это множество лучей, которое представляет собой нормальную конгруэнцию. |