Уровень: Основной текст Подробнее Глоссарии: ... Глоссарий

Лазер как нелинейная самоорганизующаяся система

Как указывалось ранее, в лазере в процессе стимулированного излучения порождаются фотоны: возбуждая атомы, мы создаем инверсию заселенности и при возвращении атома в нормальное состояние излучается свет единой фазы и частоты, т. е. происходит когерентное излучение. Если активные атомы накачиваются (возбуждаются) внешними источниками слабо, лазер действует как обычная лампа. Атомы независимо друг от друга испускают волновые цуги со случайными фазами и рассматриваются как осциллирующие диполи, колеблющиеся случайным образом. Если увеличивать накачку, то внезапно, при очень малом изменении накачки лазер переходит в новое, высокоорганизованное состояние. Атомные диполи теперь осциллируют в фазе, хотя и возбуждаются накачкой случайным образом. Таким образом, в атомной системе проявляется самоорганизация. Высокая когерентность лазерного излучения вызвана кооперативным поведением атомных диполей, т. е. Взаимосодействием.

Скорость порождения фотонов, или изменения со временем числа фотонов dn/d = определяется уравнением вида

= Прирост - Потери (1)

Прирост вызван стимулированным излучением и пропорционален числу уже имеющихся фотонов n и числу возбужденных атомов N, т. е.

Потери обусловлены уходом фотонов через торцы лазера. Допустим, что скорость ухода пропорциональна числу имеющихся фотонов, т. е.

Потери = 2 n, 2 = 1/ ₀, (3)

Число возбужденных атомов N уменьшается за счет испускания фотонов, т. е. N(n), и уравнение (1) становится нелинейным. Если в отсутствие лазерной генерации число возбужденных атомов поддерживается внешней накачкой на постоянном уровне N₀, то из-за генерации истинное число возбужденных атомов будет меньшим на величину N. Это уменьшение N пропорционально числу имеющихся в лазере фотонов n, т. к. эти фотоны постоянно заставляют атомы возвращаться в основное состояние; таким образом

N = N₀ - N, N = n. (4)

Подставляя (1) и (2) в (4), получаем основное уравнение упрощенной лазерной модели

=-kn-k₁n², k = 2 - GN₀ (5)

Если число возбужденных атомов N₀ невелико, то k положительно, а при больших N₀ коэффициент k может стать отрицательным; изменение знака происходит при

GN₀ = 2 (6)

Это условие порога лазерной генерации. Известно, что при k > 0 лазерной генерации нет, а при k < 0 возникает лазерная генерация.

Решение дифференциального уравнения (5) имеет вид

, (7)

.

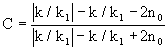Здесь n₀=n(0) - начальное состояние.

Временное поведение функции (7) таково, что она приближается к стационарному состоянию n=0 или n =|k/k₁| независимо от начального значения n₀, но в зависимости от знаков k, k₁.

В двухмодовом лазере порождаются фотоны двух типов 1 и 2 в количестве n₁ и n₂. По аналогии с (5), (6) скоростные уравнения имеют вид

N=N₀- ₁n₁ - ₂n₂

Условие стационарности

₁= ₂