







|
|
|
|
|
||
К суммирующим схемам относятся сумматоры и схемы вычитания. Их можно использовать для решения алгебраических уравнений, а также для формирования пропорционального закона в системах регулирования.
Инвертирующий сумматор формирует алгебраическую сумму двух напряжений и меняет знак на обратный.
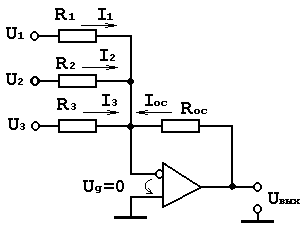
Схема алгебраического сумматора на два входа:
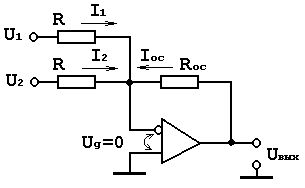
Если Rвх ОУ достаточно велико и ток смещения пренебрежительно мал по сравнению с током обратной связи (ОС), то по закону Кирхгофа :
Если коэффициент усиления без ОС также достаточно велик, так что Uд= 0, то
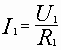 ;
; 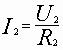 ;
; 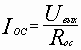 ; R1= R2= Rос= R,
; R1= R2= Rос= R, 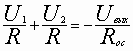 , U1+ U2= - Uвых или Uвых= -( U1+ U2).
, U1+ U2= - Uвых или Uвых= -( U1+ U2).Для n- входов
Суммирующие схемы могут работать как при постоянных, так и при переменных напряжениях.
Если отдельным входным напряжениям надо принять различные веса, то используется схема суммирования с масштабными коэффициентами.
Если ток смещения усилителя пренебрежительно мал, то согласно закону Кирхгофа
Если коэффициент усиления без ОС достаточно велик, так как Uд= 0, получим
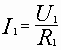 ;
; 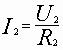 ;
; 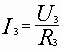 и
и 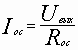 ,
, 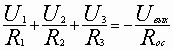
Решая это уравнение относительно Uвых получим
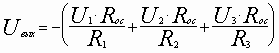 .
.Для n-входов
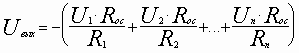
Если в последней схеме положить
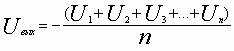 .
.Такая схема окажется схемой усреднения.
Схема на два входа:
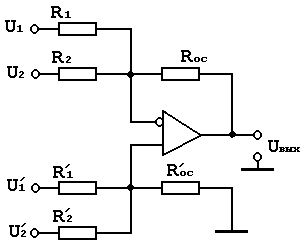
Эта схема представляет собой обобщение схемы усилителя с дифференциальным входом. Общее выражение для выходного напряжения схемы сложения вычитания очень громоздкое, рассмотрим условия необходимые для правильной работы этой схемы.
Эти условия сводятся к тому, чтобы сумма коэффициентов усиления инвертирующей части схемы была равна сумме коэффициентов усиления ее неинвертирующей части. То есть инвертирующий и неинвертирующий коэффициенты усиления должны быть сбалансированы.
Символически это можно oбозначить следующим образом:
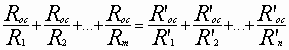
Отсюда имеем:
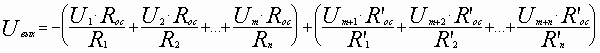
Схема на два входа:
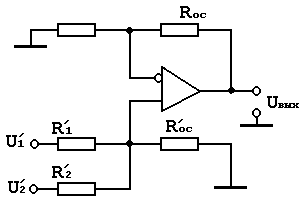
В данной схеме Uвых= U1+ U2, если
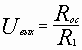 ;
; 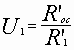 ;
; 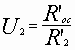 и Rос' = R1' = R2',
и Rос' = R1' = R2',Можно также осуществить суммирование с весами, при этом обязательно соблюдение условия
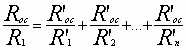 ,
,Таким образом :