







|
|
|
|
|
||
1.3. Примеры.
Пример1 Разложить рациональную дробь 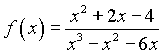 на простейшие дроби. Коэффициенты разложения найти двумя способами.
на простейшие дроби. Коэффициенты разложения найти двумя способами.
Решение.
Данная дробь - правильная (степень числителя ![]() , степень знаменателя
, степень знаменателя ![]() ,
, ![]() ).
).
I шаг. Разложим знаменатель данной дроби на простые вещественные множители:
![]() .
.
Знаменатель дроби имеет три вещественных различных корня, поэтому каждому из них будет соответствовать одна дробь.
II шаг. Напишем вид разложения данной дроби на простейшие согласно равенству (1) п.1.3 :
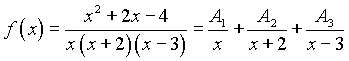 (1)
(1)
III шаг. Приведем дроби в правой части равенства (1) к общему знаменателю:
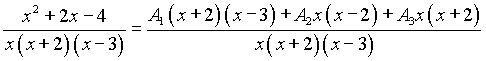 .
.
Так как равны знаменатели дробей, то равны и их числители:
![]() (2).
(2).
Теперь находим коэффициенты ![]()
Способ первый. Приравняем коэффициенты при одинаковых степенях x. Преобразуем правую часть равенства (2):
![]()
![]() , т.о. равенство (2) можно записать в виде:
, т.о. равенство (2) можно записать в виде:
![]() (3).
(3).
Приравнивая коэффициенты при одинаковых степенях x в левой и правой частях равенства (3), т.е. при ![]() (свободный член), получим систему уравнений для нахождения коэффициентов
(свободный член), получим систему уравнений для нахождения коэффициентов ![]() :
:
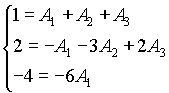
решая эту систему, получаем 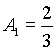 ,
, 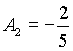 ,
, 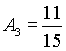 .
.
Способ второй (метод подстановки подходящих численных значений аргумента).
Подставляем в тождество (2) численные значения x. В данном случае наиболее удобно положить ![]() ,
, ![]() ,
, ![]() . Получаем:
. Получаем:
если ![]() , то
, то ![]() , следовательно,
, следовательно, 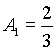
если ![]() , то
, то ![]() , следовательно,
, следовательно, 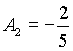
если ![]() , то
, то ![]() , следовательно,
, следовательно, 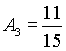
Замечание. Значения коэффициентов получаются одни и те же, независимо от способа вычисления.
Итак, исходя из равенства (1), получаем разложение данной дроби на простейшие:
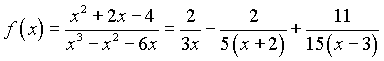
Пример2. разложить рациональную дробь 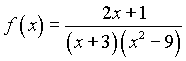 на простейшие дроби.
на простейшие дроби.
Решение.
Данная дробь правильная.
I шаг. Разложим знаменатель дроби на простейшие множители:
![]()
Знаменатель дроби имеет два вещественных корня. Корень ![]() простой и корень
простой и корень ![]() кратности 2.
кратности 2.
II шаг. Разложение данной дроби на простейшие согласно равенству (1) п.1.3 имеет вид:
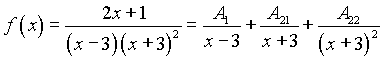 (4)
(4)
т.е. множителю ![]() соответствует одна дробь, а множителю
соответствует одна дробь, а множителю ![]() - две дроби.
- две дроби.
III шаг. Приводим дроби в правой части к общему знаменателю
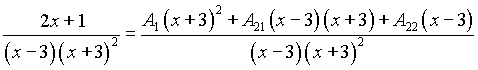 , откуда следует равенство числителей:
, откуда следует равенство числителей:
![]() (5)
(5)
IV шаг. Находим коэффициенты ![]() . Для вычисления коэффициентов используем смешанный способ ? сначала подставим в (5) значения:
. Для вычисления коэффициентов используем смешанный способ ? сначала подставим в (5) значения:
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 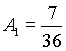
и
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 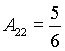
Затем приравняем коэффициенты при ![]() :
: ![]() , откуда получаем
, откуда получаем 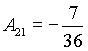 .
.
Исходя из равенства (4), получаем разложение данной дроби на простейшие:
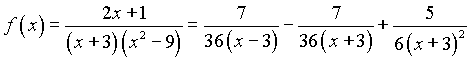
Пример3 Разложить рациональную дробь 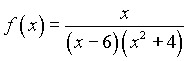 на простейшие дроби.
на простейшие дроби.
Решение.
Дробь правильная.
I шаг. Знаменатель данной дроби уже представлен в виде произведения простейших вещественных множителей, т.к. множитель ![]() не имеет вещественных корней.
не имеет вещественных корней.
II шаг. Согласно равенству (1) п.1.3 имеем:
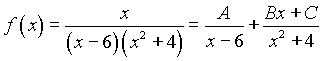 (6)
(6)
III шаг. Из тождества (6) следует тождество
![]() (7)
(7)
IV шаг. Для вычисления коэффициентов ![]() используем смешанный способ. В тождестве (7) положим:
используем смешанный способ. В тождестве (7) положим:
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 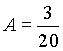
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 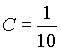
Теперь приравняем коэффициенты при ![]() в левой и правой частях тождества (7), получим:
в левой и правой частях тождества (7), получим:
![]() , следовательно,
, следовательно, 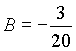
Из равенства (6) получаем разложение данной дроби на простейшие:
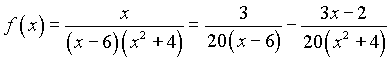
Пример4. Найти интеграл 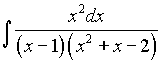 .
.
Решение.
Подынтегральная функция 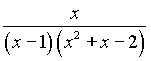 есть правильная рациональная дробь. Разложим ее на простейшие дроби. Для этого:
есть правильная рациональная дробь. Разложим ее на простейшие дроби. Для этого:
1) разложим знаменатель на простейшие вещественные множители (если это возможно).
Найдем корни множителя ![]() :
:
![]() и
и ![]()
Значит, ![]() . Тогда для знаменателя справедливо:
. Тогда для знаменателя справедливо: ![]() .
.
Таким образом, знаменатель дроби имеет только вещественные корни: простой корень ![]() и корень
и корень ![]() кратности 2.
кратности 2.
2) В соответствии с равенством (1) п.1.3 : имеем:
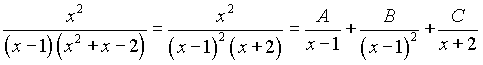 ,
,
откуда получаем тождество.
3) ![]()
4) находим коэффициенты ![]() используя смешанный метод. Сначала в тождестве 3) полагаем:
используя смешанный метод. Сначала в тождестве 3) полагаем:
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 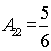
![]() , тогда
, тогда ![]() , следовательно,
, следовательно, 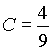
теперь приравняем свободные члены в правой и левой частях равенства 3): ![]() , откуда
, откуда 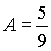 .
.
Тогда 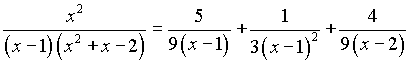
Теперь перейдем к вычислению интеграла:
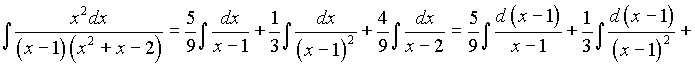
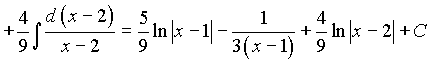
Пример5. Найти интеграл 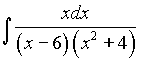 .
.
Решение.
Разложение подынтегральной дроби на простейшие имеет вид (см. пример3):
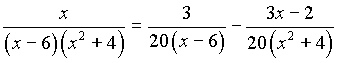 , тогда
, тогда
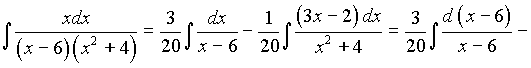
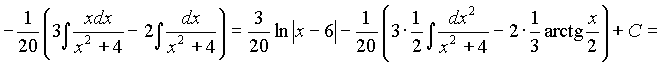
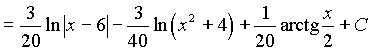 .
.