|
|
|
|
|
|
||
1. Вычислить интеграл по поверхности первого типа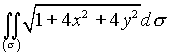 
, где 
- конечная часть поверхности 
, отсеченная плоскостью z = 0 (рис.4.10 ).
Поверхность задана уравнением, разрешенным относительно z, т. е. уравнением вида z = z(x,y), поэтому можно применить формулу (9.4). Так как
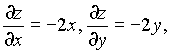
то по формуле (4.18)
Проекцией рассматриваемой части данного параболоида вращения на плоскость Оху является область, ограниченная окружностью 
(получено из уравнений поверхности и плоскости). Следовательно, областью, фигурирующей в формуле (4.19), является круг 
.
В соответствии с формулой (4.19) получаем
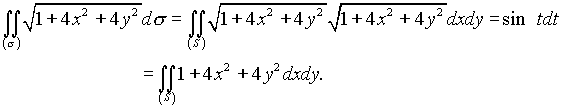
Для вычисления полученного двойного интеграла перейдем к полярным координатам
Замечая, что в области (S) 
меняется от 0 до 2
и 
- от 0 до 1, находим
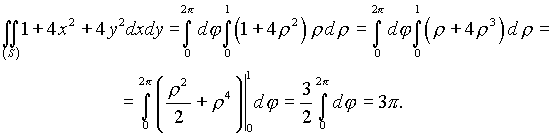
(см. упражнения )
2. Вычислить интеграл по поверхности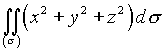 
, где - верхняя половина сферы 
(рис. 4.11)
Разрешая данное уравнение поверхности относительно z, получаем 
. По условию нужно взять знак "плюс" (рассматривается верхняя половина сферы). Таким образом, поверхность задана уравнением 
. Поскольку
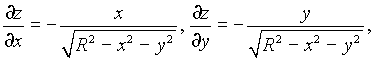
то
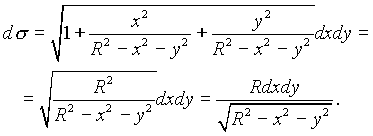
По формуле (4.19)
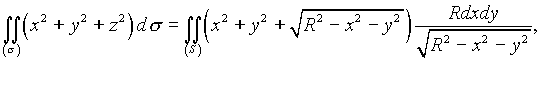
где (S) - проекция полусферы на плоскость Оху, т. е. круг 
Переходя к полярным координатам
находим
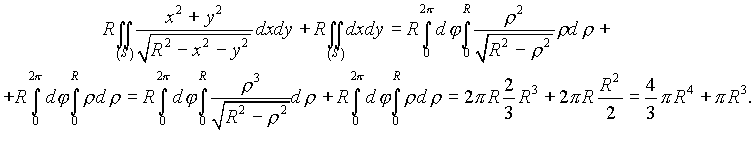
Замечание. Первый двойной интеграл вычислен с помощью подстановки 
.
(см. упражнения )
3. Вычислить интеграл по поверхности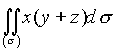 
, где - часть цилиндрической поверхности 
, отсеченной плоскостями z = 0, z = c (c>0).
Уравнение данной поверхности не содержит z, поэтому применять здесь формулу (4.19) не представляется возможным.
Так как поверхность задана уравнением, разрешенным относительна х, необходимо воспользоваться формулой
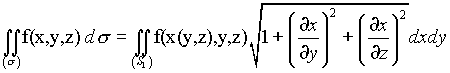
где 
проекция поверхности на плоскость Оуz. Поскольку
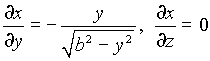
то
Заметив, что в данном случае область представляет собой прямоугольник ABCD (рис. ), определяемый неравенствами 
по указанной формуле найдем
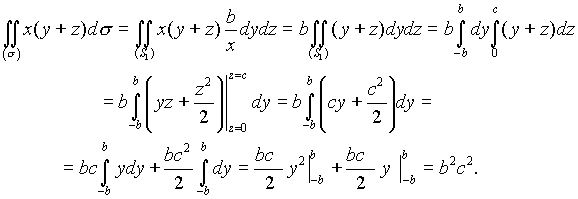
(см. упражнения )
4. Вычислить интеграл по поверхности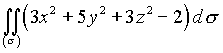 
, где - часть поверхности 
, отсеченной плоскостями 
Поверхность задана уравнением, разрешенным относительно y. Для вычисления интеграла по поверхности первого типа пользуемся формулой
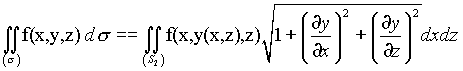
где 
- проекция поверхности на плоскость Охz.
Поскольку
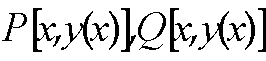
то
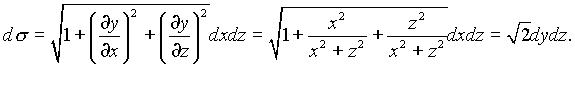
Проекцией данной поверхности на плоскость Охz является круг 
(рис. ), поэтому при переходе к полярным координатам
получим, что меняется от 0 до 2 и - от 0 до b.
По указанной формуле находим
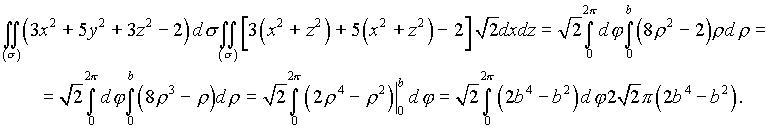
(см. упражнения )
5. Вычислить интеграл по поверхности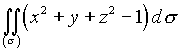 
, где - конечная часть поверхности 
отсеченной плоскостью у = 0.
Применяем формулу, приведенную в примере 4. Находим частные производные функции у по х и по z, а также элемент площади :
По указанной формуле
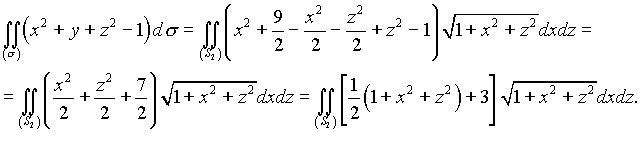
Перейдем к полярным координатам в плоскости Oxz:
Область в этой плоскости представит собой круг 
, поэтому меняется от 0 до 2 и - от 0 до 3
Следовательно,
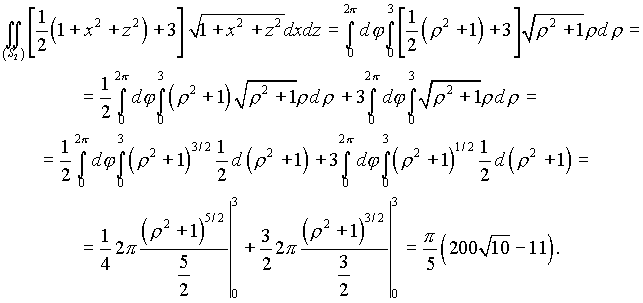
(см. упражнения )
6. Вычислить интеграл по поверхности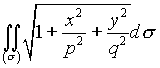 
, где - часть поверхности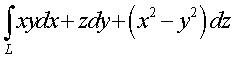 
вырезанная цилиндром 
; Имеем:
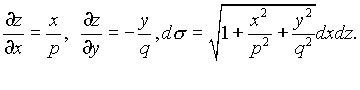
В соответствиис формулой(9.4)
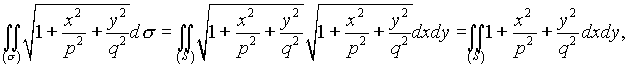
где (S)?область, ограниченная линией .
Введем обобщенные полярные координаты, положив 
Тогда
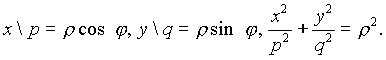
Уравнение линии, ограничивающей область S, в новых координатах примет вид
или 
Итак
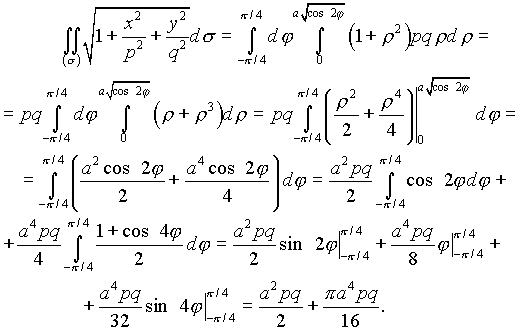
(см. упражнения )