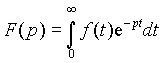 ,
,
(1)
Анализ переходных процессов даже для относительно простых цепей зачастую представляет значительные сложности, т.к. требует решения дифференциальных уравнений. Задачу можно существенно упростить, если преобразовать уравнения, сделав их алгебраическими. Но в переходных процессах во всех функциях переменной величиной является время, поэтому для исключения производных требуется перейти к новой не зависящей от времени переменной. Такой переход для функции
f(t) можно осуществить, например, с помощью преобразования Лапласа|
|
(1) |
где
p = a + jb - некоторое комплексное число, являющееся переменной функции F(p).Функция времени
f(t) называется оригиналом, а функция комплексной переменной F(p) - ее изображением.Обратный переход от изображения к оригиналу может быть осуществлен с помощью обратного преобразования Лапласа
|
|
(2) |
где интеграл вычисляется по прямой на плоскости комплексной переменной
p, проходящей параллельно мнимой оси правее всех особых точек функции F(p).Для большинства функций встречающихся в практических задачах существуют таблицы прямого и обратного преобразований и необходимость применения выражений (1) и (2) возникает крайне редко. Простейшие из этих преобразований приведены в таблице 1.
Таблица 1.
|
Оригинал |
Изображение |
Оригинал |
Изображение |
|
C |
C/p |
t |
1/p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переход от изображения к оригиналу функции может быть выполнен также с помощью формулы разложения
.Обычно изображение искомой величины
F(p) получают (или его можно представить) в виде рациональной дроби|
|
(3) |
Это выражение при условии, что
n < m и знаменатель не имеет кратных корней, можно разложить на сумму простых дробей|
|
(4) |
где
pk - корни уравнения F2(p) = 0.Определим постоянные
Ak. Для этого обе части выражения (4) умножим на (p - p1)|
|
(5) |
При
p = p1 правая часть выражения (5) равна A1, а левая становится неопределенной, т.к. F2(p1) = 0. Раскрывая неопределенность по правилу Лопиталя, получим|
|
(6) |
Следовательно, каждая постоянная в выражении (4) представляет собой отношение числителя исходной дроби к производной от знаменателя при подстановке в них соответствующего корня уравнения
F2(p) = 0. Отсюда|
|
(7) |
Оригинал функции
F(p) можно найти из выражения (7). В нем каждое слагаемое представляет некоторый постоянный коэффициент F1(pk)/F2'(pk), умноженный на функцию 1/( p - pk), оригиналом которой (см. таблицу 1) является epkt. Таким образом|
|
(8) |
Выражение (8) называется формулой разложения. Без доказательства отметим некоторые важные особенности.
|
(9) |
С помощью формулы разложения можно вычислить также начальные и конечные значения оригиналов в случае непериодического установившегося режима в виде
![]() .
.
Преобразование Лапласа является линейным преобразованием и для него справедливы следующие соотношения оригиналов и изображений
Таблица 2
|
Оригинал |
Изображение |
Оригинал |
Изображение |
|
Af(t) |
AF(p) |
|
|
|
|
|
|
|
|
|
|
|
|
где 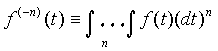 - интеграл
- интеграл
Важнейшим свойством преобразования Лапласа, позволяющим алгебраизировать дифференциальные уравнения оригиналов, является то, что при нулевых начальных значениях функции и всех ее производных операции дифференцирования оригинала соответствует умножение изображения
на p, а операции интегрирования - деление.В электрических цепях производными и интегралами выражаются токи и напряжения реактивных элементов
L и C. Найдем для них изображения падений напряжения.Напряжение на индуктивности равно  . Воспользовавшись выражением для производной таблицы 2, получим изображение этого напряжения в виде
. Воспользовавшись выражением для производной таблицы 2, получим изображение этого напряжения в виде
|
|
(10) |
где
i(0) - значение тока в момент коммутации. Произведение pL связывает между собой изображения тока и напряжения при нулевых начальных условиях и может рассматриваться как изображение индуктивности L. Величина Li(0) является константой и имеет размерность изображения падения напряжения. Следовательно, ее в области изображений можно представить источником постоянной ЭДС равной Li(0).С помощью таблицы 2 можно найти изображение падения напряжения на емкости
|
|
(11) |
где
uC(0) - значение напряжения на емкости в момент коммутации. Величина 1/(pC) в выражении (11) связывает между собой изображения тока и напряжения при нулевых начальных условиях и может считаться изображением емкости C. Второе слагаемое изображения напряжения величина постоянная и может быть представлена в области изображений соответствующим источником ЭДС.Для резистора связь между током и напряжением в области оригиналов соответствует умножению тока на постоянную величину
R. Поэтому изображение напряжения на резисторе будет равно произведению изображения тока на константу R.Выражения (10) и (11) позволяют представить электрической схемой изображения величин.
Электрическая схема, в которой все величины и элементы представлены изображениями называется операторной схемой замещения. Пассивные элементы электрической цепи и их схемы замещения приведены в таблице 3.Таблица 3.
|
Оригинал |
Изображение |
||
|
|
u = Ri |
|
U(p) = RI(p) |
|
|
|
|
U(p) = pLI(p)- Li(0) |
|
|
|
|
|
Таким образом, операторную схему замещения можно получить из электрической схемы цепи, если в ней все элементы заменить изображениями в соответствии с таблицей 3, а источники электрической энергии представить источниками, у которых оригинальная ЭДС или ток заменены их изображением по Лапласу.
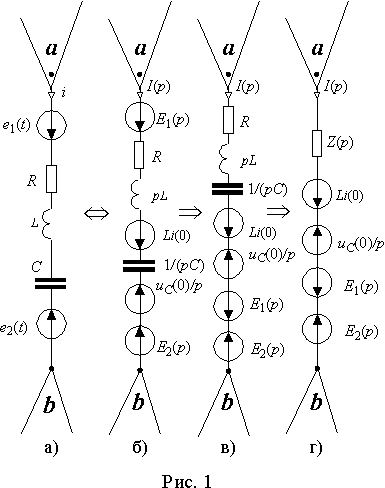
Проделаем эту операцию для ветви, показанной на рис. 1 а). В нее включены все элементы электрической цепи, которые могут входить в последовательное соединение.
Заменяя в ветви все пассивные элементы их изображениями и включив в нее источники ЭДС, соответствующие начальным значениям тока в индуктивности и напряжения на емкости в момент коммутации, мы получим операторную схему замещения, представленную на рис. 1 б).
Перегруппируем элементы, так, чтобы изображения пассивных элементов находились вместе и, пользуясь свойствами линейного преобразования (
таблица 2), запишем выражение для изображения падения напряжения между узлами a и b в виде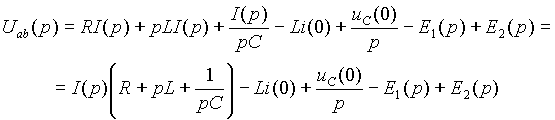
Выражение
Z(p)=R+pL+1/(pC) называется операторным сопротивлением участка цепи. Нетрудно заметить, что оно равно комплексному сопротивлению, если в нем оператор p заменить на jw . Отсюда изображение тока в ветви|
|
(12) |
Выражение (12) называется законом Ома в операторной форме. Очевидно, что название это происходит от формальной аналогии, т.к. Ом не исследовал переходные процессы в электрической цепи. При отсутствии в цепи источников ЭДС и запасов энергии в электрических и магнитных полях выражение (12) преобразуется к виду
|
|
(13) |
В электрических цепях первый закон Кирхгофа устанавливает связь между токами в узлах в виде равенства нулю их алгебраической суммы. Применяя к сумме преобразование Лапласа, можно убедиться в том, что в области изображений также справедлив закон, имеющий форму первого закона Кирхгофа
|
|
(14) |
Второй закон Кирхгофа устанавливает связь между падениями напряжения в замкнутом контуре электрической цепи и ЭДС, действующими в этом контуре. По форме он представляет собой сумму этих величин и, следовательно, может быть линейно преобразован по Лапласу в виде
|
|
(15) |
где
q и w - соответственно число индуктивностей и емкостей в контуре с ненулевыми начальными значениями. Выражение второго закона Кирхгофа для изображений отличается от записи для оригиналов наличием дополнительных ЭДС, соответствующих начальным значениям токов в индуктивностях и напряжений на емкостях. Если же применять этот закон к операторной схеме замещения, где начальные значения учтены источниками ЭДС, то формально составление уравнений будет полностью аналогично области оригиналов, только число источников будет больше на число ненулевых начальных значений.На примере законов Ома и Кирхгофа мы убедились, что формы записи и методы составления уравнений в области изображений полностью аналогичны тем, которые используются во временной области. Эту аналогию можно распространить и на другие способы анализа электрических цепей в применении к изображениям. Теперь можно следующим образом описать общий алгоритм анализа переходных процессов операторным методом:
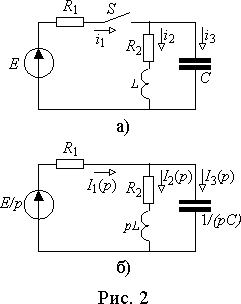
Найдем токи протекающие в электрической цепи рис. 2 а) после замыкания ключа, если
E = 100 В, R1 = 20 Ом, R2 = 5 Ом, L = 100 мГн , C = 10 мкФ и в момент коммутации емкость была полностью разряжена.Так как до замыкания ключа
S ток в индуктивности и напряжение на емкости были равны нулю, то в операторной схеме замещения не будет источников ЭДС, соответствующих начальным значениям, и она будет иметь вид, представленный на рис. 2 б).Общее операторное сопротивление цепи равно
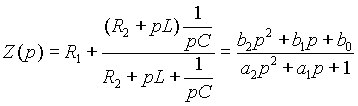 ,
,
где
b2 = R1LC; b1 = L+R1R2C; b0 = R1+R2; a2 = LC; a1 = R2C.Изображение тока
I1(p) по закону Ома будет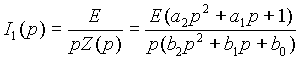
Приравняв нулю знаменатель этого выражения, мы, как и следовало ожидать, получим нулевой корень, соответствующий действию в цепи источника постоянной ЭДС, и еще два корня
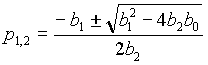
при данных задачи равные
p1 = - 261 и p2 = - 4789. Таким образом, переходный процесс в цепи апериодический и будет продолжаться 3t 1 = 3/261 = 11.5 мс.Для определения оригинала тока воспользуемся
выражением (9). Тогда ток i1 будет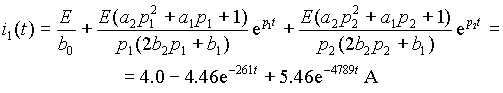
Определим теперь ток в емкости. Его изображение с помощью закона Ома можно представить в виде
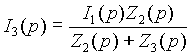 ,
,
где
Z2(p) = R2+pL и Z3(p) = 1/(pC) операторные сопротивления соответствующих ветвей. Подставив выражение для I1(p), получим изображение I3(p)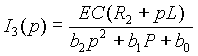
и, по формуле разложения, оригинал
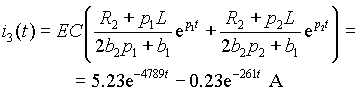
Ток в индуктивности проще всего найти, воспользовавшись первым законом Кирхгофа
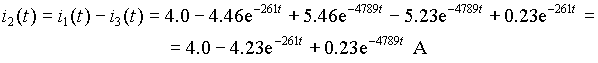
Таким образом, ток в емкости
i3 в момент коммутации скачком возрастает от гуля до 5.0 А, а затем апериодически спадает до нуля. Ток в индуктивности i2 в момент коммутации равен нулю и далее монотонно возрастает до установившегося значения, равного 4.0 А. Входной ток после замыкания ключа скачком возрастает до 5.0 А и со временем снижается до 4.0 А.