(1)
В тех случаях, когда требуется учесть процессы в электрическом и магнитном поле электрическая цепь содержит реактивные элементы обоих типов. Простейшим вариантом такой цепи является последовательное соединение
R-L-C (рис. 1).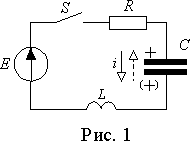
Уравнение Кирхгофа для этой цепи после замыкания ключа S
|
(1) |
Возьмем производную по времени от обеих частей уравнения
|
|
(2) |
Характеристическое уравнение для дифференциального уравнения (2) можно получить заменой производных по времени на
pk|
|
(3) |
где 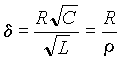 - величина, названная при рассмотрении
- величина, названная при рассмотрении
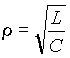 - волновое сопротивление цепи, а
- волновое сопротивление цепи, а 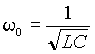 - угловая частота, на которой в цепи рис. 1 возникает резонанс.
- угловая частота, на которой в цепи рис. 1 возникает резонанс.
Корнями этого характеристического уравнения являются
|
|
(4) |
Таким образом, корни характеристического уравнения являются функцией затухания
d и резонансной частоты w 0, значения которых, в свою очередь, определяются параметрами цепи R, L и C. Резистивное сопротивление R входит только в выражение для затухания и при вариации R резонансная частота будет сохраняться постоянной. Поэтому при анализе корней затухание можно считать независимой переменной, а резонансную частоту константой, т.к. эти условия можно реализовать изменением R.Из выражения (4) следует, что корни могут быть вещественными отрицательными, если
d і 2, или комплексно-сопряженными, если d < 2. Для первого случая их можно представить в виде|
|
(5) |
где 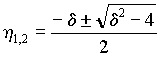 , а для второго в виде
, а для второго в виде
|
|
(6) |
где
s = - d /2 и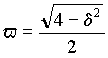 . Безразмерные величины s и v можно назвать относительным затуханием и относительной частотой, т.к. они связаны с абсолютными значениями этих величин через резонансную частоту w 0.
. Безразмерные величины s и v можно назвать относительным затуханием и относительной частотой, т.к. они связаны с абсолютными значениями этих величин через резонансную частоту w 0.
Если затухание цепи
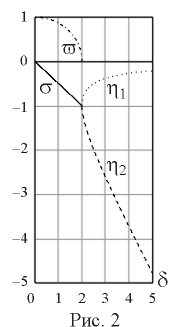
d і 2, то оба корня отрицательные вещественные различные (кроме предельного случая d =2) и свободные составляющие всех величин в переходном процессе будут суммой двух экспонент с различными показателями. Значения тока и напряжений со временем не будут регулярно повторяться, поэтому такой переходный процесс называется апериодическим. Так как p1,2 < 0, то обе экспоненты будут со временем уменьшаться до нуля со скоростью, определяемой постоянной времени каждой из них t 1,2 = 1/| p1,2 | = 1/(w 0|h 1,2|). Таким образом, чем больше абсолютное значение h , тем быстрее закончится переходный процесс. Для двух экспонент длительность процесса будет определяться меньшим абсолютным значением h . Из рис. 2 следует, что при увеличении затухания d значения h 1 и h 2 расходятся, причем при d (r) µ h 1 (r) 0 и длительность переходного процесса становится бесконечной. Одновременно h 1 и h 2 достигают наибольших возможных абсолютных значений в предельном режиме, когда d =2. Следовательно, этот режим будет соответствовать минимальной длительности переходного процесса в цепи.При затухании
0 < d < 2 корни характеристического уравнения комплексно-сопряженные с отрицательной вещественной частью. В этом случае свободная составляющая решения дифференциального уравнения также будет суммой двух экспонент, но эти экспоненты могут быть объединены и решение получено в видеa(t) = Aes tsin(v t+n )
Эта функция представляет собой синусоиду с изменяющейся во времени амплитудой. Всякая синусоидальная функция соответствует колебаниям величины относительно среднего значения, поэтому переходный процесс в цепи называется колебательным. Вещественная часть корней характеристического уравнения
s определяет скорость изменения амплитуды, а мнимая v , частоту колебаний. Следовательно, длительность переходного процесса будет зависеть только от s = - d /2. Так как s < 0, то со временем амплитуда колебаний свободной составляющей будет уменьшаться. При уменьшении затухания d абсолютное значение s также уменьшается, что соответствует увеличению длительности переходного процесса. Максимального абсолютного значения равного s = h 1 = h 2 = - 1 (рис. 2) s достигает в предельном режиме при d (r) 2, подтверждая сделанное ранее утверждение, что в этом режиме длительность переходного процесса минимальна.Для оценки скорости изменения свободных составляющих в колебательном переходном процессе можно сравнить между собой два значения, отстоящих друг от друга на время равное периоду колебаний
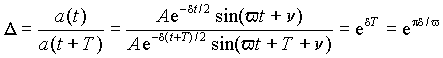 .
.
Величина
D называется декрементом колебаний. На практике чаще применяют натуральный логарифм D называемый логарифмическим декрементом колебаний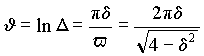 .
.
Как и следовало ожидать, скорость изменения свободных составляющих в колебательном переходном процессе зависит только от затухания электрической цепи
.Частота колебаний свободных составляющих тока и напряжений при изменении затухания также изменяется. При увеличении затухания она стремится к нулю (
рис. 2), а при уменьшении к резонансной частоте цепи. При отсутствии затухания в цепи будет протекать переменный синусоидальный ток с частотой w0.
Рассмотрим теперь процесс подключения цепи
рис. 1 к источнику постоянной ЭДС E. Емкость C при этом может быть полностью разряжена или заряжена до напряжения U0 , которое с помощью коэффициента - µ < c < +µ можно представить через ЭДС источника в виде U0 = cE. При c < 1 ток в цепи после замыкания ключа будет протекать в направлении показанном сплошной стрелкой.Установившееся значение тока в цепи будет равно нулю, а установившееся значение напряжения на емкости - ЭДС
E. В общем случае напряжение на емкости при переходном процессе равно![]() ,
,
а ток в цепи
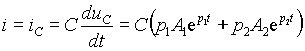
Постоянные интегрирования
A1 и A2 нужно определить из начальных значений тока и напряжения на емкости в момент коммутации, пользуясь тем, чтоuC(0-) = U0 = cE = uC(0+) = E + A1 + A2 и
i(0-) = 0 = i(0+) = C(p1A1 + p2A2) .
Отсюда
A1 = E(1- c)p2/( p1- p2) и A2 = - E(1- c)p1/( p1- p2) . Подставляя полученные значения в выражения для напряжения на емкости и тока получим|
|
(7) |
|
|
(8) |
Если в выражения (7) и (8) подставить корни характеристического уравнения из
выражения (5), то для апериодического процесса напряжение на емкости и ток в цепи будут|
|
(9) |
|
|
(10) |
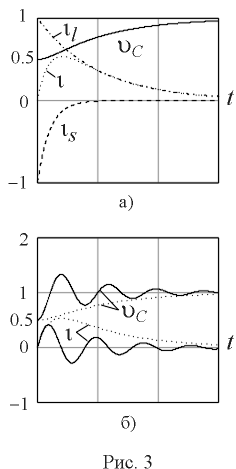
На рис. 3 а) приведены эти кривые при относительном начальном значении напряжения на емкости
c = 0.5. В качестве базовых значений для напряжения принята ЭДС E, а для тока E(1- c)/[Lw 0(h 1- h 2)]. Для тока также построены быстро и медленно затухающие составляющие экспоненты is и il (i =is+il).Выражения (7) и (8) получены без введения каких-либо ограничений на корни характеристического уравнения. Поэтому для нахождения решения при колебательном процессе
(d <2) можно подставить корни из выражения (6), а затем преобразовать полученную сумму экспонент с комплексными показателями по формуле Эйлера. В результате мы получим выражения для напряжения на емкости и тока в цепи в виде|
|
(11) |
|
|
(12) |
где
y = arctg(v /s ) = arctg(2p /J ) .На рис. 3 б) приведены кривые
колебательного переходного процесса при том же относительном начальном значении напряжения на емкости c, что и при апериодическом процессе (они построены на рисунке пунктиром).