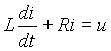Рассмотрим переходные процессы в цепи, содержащей последовательно соединенные резистор R и индуктивность L . Уравнение Кирхгофа для такой цепи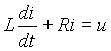

,

где u = u(t) - напряжение на входе цепи. Найдем решение этого уравнения для свободной составляющей тока, т.е. при u = 0, в виде i_с = Ie^pt . Для этого подставим выражение для тока в исходное уравнение и найдем значение p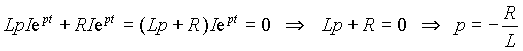

.

Выражение Lp + R=0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных тока на p^k, где k - порядок производной.

Таким образом, общее решение для тока при переходном процессе в R-L цепи можно представить в виде

где t = 1/|p| = L/R - постоянная времени переходного процесса; I - постоянная интегрирования, определяемая по начальным значениям; i - установившийся ток в цепи, определяемый по параметрам R и L и напряжению на входе u.

Длительность переходного процесса в цепи, определяемая значением t , возрастает с увеличением L и уменьшением R.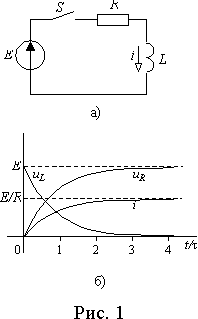

Рассмотрим подключение R-L цепи к источнику постоянной ЭДС E (рис. 1 а)).

Установившийся ток в этой цепи будет определяться только ЭДС E и резистивным сопротивлением R, т.к. после окончания переходного процесса i = const и u_L = Ldi/dt = 0, т.е. i_у = E/R .

.

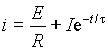Для определения постоянной I найдем начальное тока. До замыкания ключа ток очевидно был нулевым, а т.к. подключаемая цепь содержит индуктивность, ток в которой не может измениться скачкообразно, то в первый момент после коммутации ток останется нулевым. Отсюда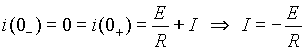

.

Подставляя найденное значение постоянной I в выражение для тока, получим

Из этого выражения можно определить падения напряжения на резисторе u_R и индуктивности u_L

Из выражений (1)-(3) следует, что ток в цепи нарастает по экспоненте с постоянной времени t = L/R от нулевого до значения E/R (рис. 1 б)). Падение напряжения на сопротивлении u_R повторяет кривую тока в измененном масштабе. Напряжение на индуктивности u_L в момент коммутации скачкообразно возрастает от нуля до E , а затем снижается до нуля по экспоненте (рис. 1 б)).

.

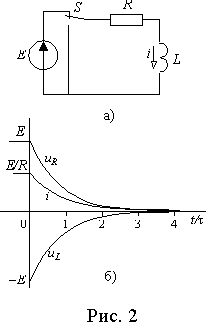
Пусть рассмотренная выше R-L цепь длительное время была подключена к источнику ЭДС E, а затем замкнута накоротко (рис. 2 а)).

В этом случае установившийся ток будет равен нулю и задача сводится к отысканию его свободной составляющей. Из выражения (1)

.

Постоянную I можно определить из начальных условий. Установившийся ток в цепи до переключения ключа S был равен i(0- ) = E/R, а т.к. в первый момент после коммутации ток в индуктивности сохраняет свое значение, то i(0- ) =i(0₊) = I = E/R . Отсюда ток и падения напряжения в цепи

Из выражений (4) следует, что при замыкании цепи накоротко ток уменьшается от E/R до нуля по экспоненте с постоянной времени t = L/R (рис. 2 б)). Падение напряжения на резисторе изменяется по такому же закону, а напряжение на индуктивности в момент коммутации скачком изменяется от нуля до - E, а затем снижается до нуля ( рис. 2б)).

,

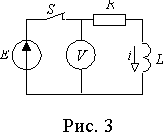
При отключении цепи содержащей индуктивность в ней могут возникать падения напряжений опасные для ее элементов. Пусть R-L цепь с подключенным к ней вольтметром отключается от источника постоянной ЭДС E (рис. 3).

Так как цепь содержит индуктивность, то после размыкания ключа S ток не сможет изменить своего значения и будет протекать в контуре R-L-V . Значение тока до коммутации i(0- ) = E/R = i(0₊) = i(0) Уравнение Кирхгофа для этого контура

Ri + R_Vi + u_L = 0,

где R_V - сопротивление вольтметра.

Отсюда падение напряжения на вольтметре u_V = R_V i(0) = ER_V/R и на индуктивности u_V = (R+R_V)i(0) = E(1+R_V/R).

Обычно R_V>>R , поэтому напряжение на вольтметре и на индуктивности в момент отключения превосходят ЭДС источника в R_V/R раз. Это может быть опасным для вольтметра и изоляции катушки. Если индуктивность цепи достаточно велика, то запасенной в ней энергии может оказаться достаточно для разрушения изоляции или входных цепей прибора. Поэтому при отключении цепи постоянного тока с большой индуктивностью ее предварительно замыкают на малое сопротивление, а измерительные приборы отключают.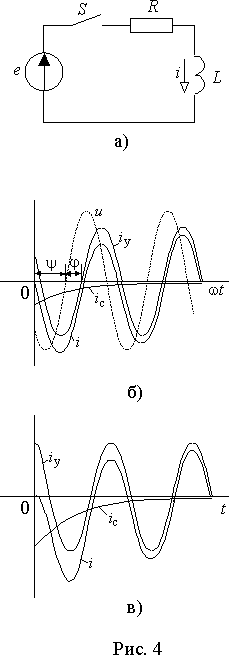

Рассмотрим теперь процесс подключения R-L цепи к источнику переменной синусоидальной ЭДС (рис. 4 а)).

Ток после коммутации в соответствии с выражением (1)

Установившееся значение i_у определяется по закону Ома как

где y - фаза напряжения на входе цепи в момент коммутации, а j = arctg(w L/R) .

До коммутации ток в цепи был равен нулю, поэтому из выражений (5) и (6) можно найти постоянную I

,

Таким образом, ток в цепи состоит из двух составляющих - установившегося периодического синусоидального тока и свободного, уменьшающегося по экспоненте с постоянной времени t = L/R (рис. 4 б)). В результате, ток в некоторые моменты времени превышает амплитудное значение установившегося тока.

Начальное значение свободной составляющей тока I_msin(y - j ) зависит от момента включения y . При y = j +(k+1/2)p (k = 0, 1, 2ј ) ток через полпериода после коммутации (рис. 4 в)) достигает максимального значения, равного I_max=I_m[1+e- p ^t/(w t )]. Значение e- p ^t/(w t )<1, поэтому и максимум не превышает двойной амплитуды установившегося тока. Конкретное значение зависит от частоты источника питания w и постоянной времени t . При w ® µ и/или t ® µ I_max ® 2.

При y = j + kp (k = 0, 1, 2ј ) свободный ток в момент коммутации равен нулю и переходный процесс отсутствует. В цепи сразу после коммутации возникает установившийся режим. Эта особенность переходных процессов на переменном токе используется в устройствах детерминированного включения. В них момент включения нагрузки выбирают таким образом, чтобы уменьшить или исключить большие значения тока, напряжения или других параметров.

Перейдем к рассмотрению переходных процессов в цепи с последовательным соединением резистора R и емкости C. По второму закону Кирхгофа для этой цепи

Ri + u_C = u.

Ток в емкости можно представить в виде i = Cdu_C/dt. Отсюда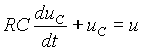

.

Решение этого дифференциального уравнения для напряжения на емкости также можно представить суммой свободной и установившейся составляющих u_C = u_у + u_с. Свободную составляющую найдем из решения однородного уравнения (u = 0) в виде u_с = Ue^pt. Подставим это выражение в уравнение и найдем значение p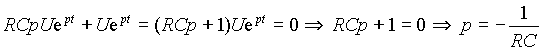

Выражение RCp + 1 = 0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных от напряжения на емкости на p^k, где k - порядок производной.

где U - постоянная интегрирования, определяемая из начальных значений; t = 1/|p| = RC - постоянная времени переходного процесса.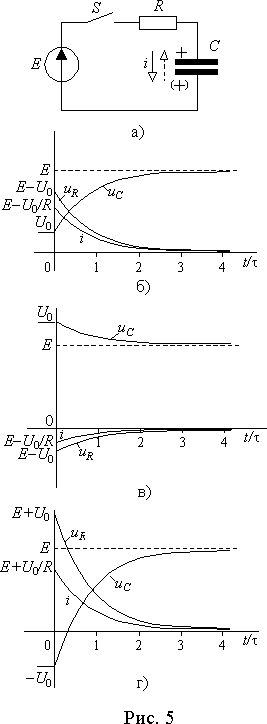

Рассмотрим процесс подключения последовательной R-C цепи к источнику постоянной ЭДС E (рис. 5 а)).

В отличие от индуктивности, емкость после накопления заряда может длительное время сохранять его. Поэтому начальное значение напряжения на емкости U₀ может быть произвольным и иметь произвольный знак по отношению к ЭДС источника.

Установившееся значение напряжения на емкости после замыкания ключа S всегда будет равно E, т.к. на постоянном токе в установившемся режиме du_C/dt = 0 и i = Cdu_C/dt = 0, а u_C = u - Ri = E - Ri = E. Поэтому из выражения (8) напряжение на емкости в общем виде будет равно

Пусть напряжение на емкости до коммутации было u_C(0- ) = ± U₀ (знак + соответствует полярности напряжения на рис. 5 а) без скобок). Тогда из (9) для момента времени непосредственно после замыкания ключа найдем постоянную U

,

где t = RC - постоянная времени переходного процесса.

На рис. 5 б)-г) приведены временные диаграммы переходного процесса подключения R-C цепи к источнику постоянной ЭДС для трех вариантов начальных значений напряжения на емкости: 1) E > U₀ > 0 ; 2) E < U₀ и U₀ > 0; 3) U₀ < 0 Во всех случаях напряжение на емкости монотонно по экспоненте изменяется отU₀ до E. В то время как ток и напряжение на резисторе в момент коммутации скачкообразно изменяются на величину пропорциональную разности или сумме E и U₀, а затем монотонно уменьшаются до нуля. При этом, если E < U₀, то ток и падение напряжения на R отрицательны, т.е. происходит разряд емкости.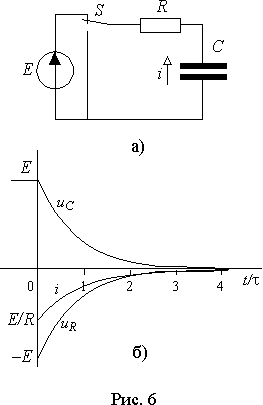

Полный разряд емкости происходит при отсутствии внешних источников энергии (рис. 1 а)). После переключения ключа S вся энергия накопленная в электрическом поле емкости C преобразуется в тепло в резисторе R.

u_C = u_с= Ue- ^t/t

и если цепь достаточно длительное время была подключена к источнику, то в момент переключения напряжение на емкости будет равно E. Поэтому постоянная U будет равна

u_C(0- ) = E = u_C(0₊) = U,