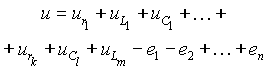
(1)
В последовательное соединение в цепях переменного тока кроме резисторов могут входить реактивные элементы - индуктивности и емкости.
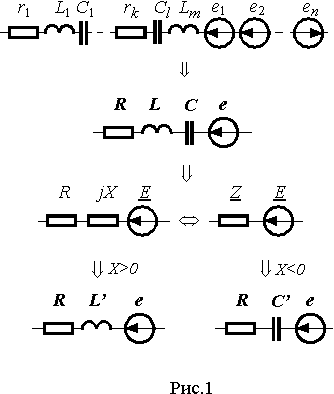
Пользуясь понятием потенциала, падение напряжения на последовательном соединении (рис. 1) можно представить суммой падений напряжений на отдельных элементах
|
|
(1) |
Последовательное соединение не содержит узлов, поэтому по всем его элементам протекает одинаковый ток. Пусть этот ток равен
i=Imsinwt, тогда, с учетом выражений для падения напряжения на реактивных элементах, выражение (1) преобразуется к виду|
|
(2) |
Таким образом, в последовательном соединении все резисторы, индуктивности и емкости можно заменить эквивалентными элементами
R, L и C , причем|
|
(3) |
Из выражений (3) следует, что эквивалентные сопротивление и индуктивность больше наибольшего из значений параметров элементов, входящих в соединение, а эквивалентная емкость - меньше наименьшего из значений. Иначе говоря, последовательное подключение в цепь сопротивления или индуктивности увеличивает их эквивалентные значения, а последовательное подключение емкости - уменьшает.
Рассмотренные выше преобразования последовательного соединения не затрагивали входящих в него источников ЭДС. Это связано с тем, что во временной области ЭДС являются синусоидальными функциями с различными начальными фазами. Поэтому их преобразование лучше провести, перейдя к изображениям комплексными числами и векторами.
Как известно, операции суммирования в области оригиналов соответствует суммирование и в области изображений. Отсюда
|
|
(4) |
где
E и e - изображение и оригинал эквивалентного источника ЭДС, т.е. любое количество последовательно соединенных источников ЭДС можно заменить одним эквивалентным, значение ЭДС которого равно алгебраической сумме ЭДС, входящих в соединение.После того, как резисторы, индуктивности, емкости и ЭДС заменены эквивалентными параметрами и элементами можно определить комплексное сопротивление пассивных элементов
|
|
(5) |
Мнимая часть комплексного сопротивления
Z может быть положительной или отрицательной в зависимости от того какое сопротивление больше, индуктивное xLили емкостное xC . При положительном значении реактивной составляющей комплексного сопротивления X, соединение L-C можно представить индуктивностью L', реактивное сопротивление которой xL' равно X . Отсюда значение эквивалентной индуктивности|
|
(6) |
где
L и C - значения эквивалентной индуктивности и емкости, определенные из выражений (3). В случае X<0 , реактивные элементы, входящие в последовательное соединение можно представить эквивалентной емкостью|
|
(7) |
Таким образом, в случае заданного значения частоты
последовательное соединение можно представить последовательным соединением резистора, реактивного элемента и источника ЭДС, параметры которых определяются по выражениям (3), (4), (6) и (7). Резистор, реактивный элемент и источник ЭДС являются минимальным набором элементов, с помощью которых можно представить последовательное соединение. При наличии в цепи реактивных элементов обоих типов (индуктивности и емкости) в минимальном наборе элементов (минимальной эквивалентной схеме) будет присутствовать только один из них.При отсутствии каких-либо элементов в исходной схеме, например резисторов или источников ЭДС, будут отсутствовать и соответствующие компоненты эквивалентного представления.
Перейдем теперь к рассмотрению параллельного соединения элементов цепей переменного тока.
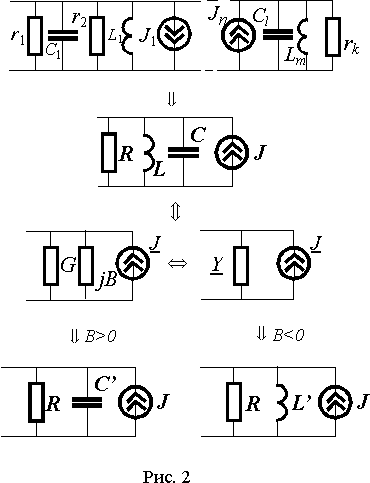
В параллельное соединение (рис. 2) могут входить резистивные и реактивные элементы, а также источники тока.
Источники ЭДС не могут соединяться параллельно, т.к. , если два источника
e1 и e2 подключены к узлам a и b, то uab= e1 и uab= e2 , что возможно только при e1 = e2.Общий ток, протекающий через соединение в целом, представляет собой сумму токов, протекающих через отдельные элементы. Поэтому можно написать
|
|
(8) |
Все элементы соединения подключены к двум узлам, разность потенциалов которых является падением напряжения на каждом элементе. Пусть это напряжение u равно
Umsinw t. Тогда|
|
(9) |
Из выражения (9) следует, что в параллельном соединении все резисторы, индуктивности и емкости можно заменить эквивалентными элементами
R , L и C , значения которых определяются выражениями|
|
(10) |
Из этих выражений следует, что параллельное подключение резистора или индуктивности уменьшает их эквивалентные значения, а параллельное подключение емкости - увеличивает эквивалентную емкость. Эквивалентное сопротивление
R и индуктивность L всегда меньше наименьшего из параметров элементов, образующих соединение. В то время как эквивалентная емкость C - больше, чем самая большая емкость параллельного соединения.Для определения тока эквивалентного источника воспользуемся представлением токов комплексными числами аналогично тому, как это было сделано для ЭДС последовательного соединения
|
|
(11) |
т.е. путем перехода к изображениям в виде комплексных чисел, а зетам обратного перехода во временную область можно получить параметры эквивалентного источника тока
J, заменяющего собой все источники входящие в соединение.Комплексная проводимость соединения может быть выражена через эквивалентные параметры следующим образом
|
|
(12) |
В зависимости от соотношения значений емкостной и индуктивной проводимостей
bL и bC , реактивная составляющая комплексной проводимости B может быть положительной или отрицательной. В первом случае, параллельное соединение L-C можно представить емкостью C', проводимость которой равна B. Во втором случае, реактивную проводимость можно создать эквивалентной индуктивностью L'. Значения L' и C' можно определить как|
|
(13) |
Следовательно, при заданной частоте
параллельное соединение, также как и последовательное, можно представить минимальным набором элементов, включающим параллельно соединенные резистор, реактивный элемент и источник тока. Тип реактивного элемента (индуктивность или емкость) определяется знаком эквивалентной реактивной проводимости.Следует особо подчеркнуть, что
выражения (3) и (10) не содержат частоты w в качестве параметра. Поэтому они справедливы всегда и применяются как для расчетов, так и при операциях с реальными объектами. Например, две соединенные последовательно катушки индуктивности в 40 и 60 мГн можно заменить одной с индуктивностью в 100 мГн. В то же время, переход к одному реактивному элементу (выражения (6), (7) и (13)) возможен только для конкретного значения частоты и применяется чаще всего в расчетных задачах.