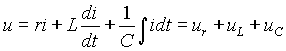Рассмотрим электрическую цепь состоящую из последовательно включенных сопротивления r, индуктивности L и емкости C (рис. 1 а)).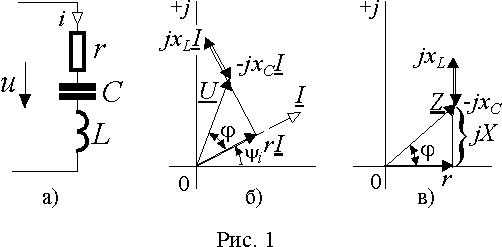

Протекающий ток i создает на всех элементах цепи падения напряжения, сумма которых равна напряжению на входе u. Для синусоидальных функций времени это можно записать в виде выражения

Пусть ток в цепи равен i = I_msin(wt+y_i). Подставим это выражение в (1) и получим:

Очевидно, что определить из выражения (2) амплитуду и начальную фазу напряжения u сложно. Поэтому перейдем в выражении (1) от оригиналов величин к их символическим изображениям комплексными числами или векторами.

Формально выражение (3) совпадает с записью закона Ома для цепи постоянного тока. Отличие заключается в том, что все величины входящие в него являются комплексными числами изображающими реальные функции времени. Поэтому его можно назвать законом Ома в области изображений.

Графически выражение (3) можно представить векторной диаграммой рис. 1 б). Здесь вектор входного напряжения U складывается из трех составляющих. Вектор падения напряжения на резистивном сопротивлении rI совпадает по направлению с током I , т.к. отличается от него только вещественным коэффициентом r . Вторая составляющая jx_LI перпендикулярна вектору тока I и опережает его по фазе на 90°. Это связано с умножением на оператор поворота j вектора x_LI , совпадающего по направлению с током. Третий вектор -jx_СI отстает по фазе от тока на 90° , т.к. образуется из него умножением на оператор поворота -j .

Величина Z = r+j(x_L- x_C) = r+jx = Ze ^jj в выражении (3), имеющая размерность сопротивления, называется комплексным сопротивлением. Его вещественная часть r называется резистивным сопротивлением, а мнимая x = x_L- x_C - реактивным сопротивлением. Из выражения (3) следует, что комплексное сопротивление является отношением комплексного падения напряжения к комплексному току

поэтому его модуль Z можно определить через отношение модулей напряжения и тока Z=U/I или через резистивную и реактивную составляющую . Модуль комплексного сопротивления называется полным сопротивлением.

Аргумент комплексного сопротивления j есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как j = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи. Из выражения (4) необходимо следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные - опережению.

Теперь можно вернуться к определению оригинала напряжения u на входе цепи рис. 1 а) преобразованием изображения (5) -

Из выражения (3) можно представить комплексное сопротивление суммой трех величин в виде

и изобразить эти соотношения на векторной диаграмме (рис. 1 в)). Векторная диаграмма сопротивлений подобна векторной диаграмме напряжений, т.к. комплексное сопротивление Z аналитически можно получить делением комплексного напряжения U на комплексный ток I . Графически это соответствует повороту векторной диаграммы напряжений на угол -y _i и изменению ее масштаба на 1/I.

Величина Y называется комплексной проводимостью. Ее модуль является величиной обратной модулю комплексного сопротивления, а аргумент всегда равен его аргументу, но имеет противоположный знак.

Вещественная составляющая комплексной проводимости называется резистивной проводимостью, а мнимая - реактивной проводимостью.

Между резистивными (R и G) и реактивными (X и B)составляющими комплексной проводимости и сопротивления существует очевидное соответствие, вытекающее из понятия комплексного числа.

 ЗАДАЧА 1

Угол сдвига фаз между напряжением и током в электрической цепи определяется аргументом ее комплексного сопротивления j . Поэтому при анализе цепи часто бывает достаточно определить характер изменения этого угла при вариации некоторого параметра.

Комплексное сопротивление любого участка электрической цепи в общем случае имеет вещественную и мнимую составляющие Z=R+jX. Построим вектор Z на комплексной плоскости и проанализируем его поведение при вариации составляющих R и X .

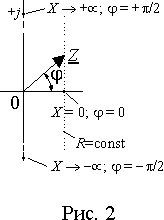
Пусть R=const, а X=var. Тогда конец вектора Z будет скользить по прямой R=const (рис. 2). При X = 0 сопротивление Z вещественное, т.е. чисто резистивное и сдвиг фаз между током и напряжением j равен нулю.

Если X(r) µ , то вектор Z поворачивается в положительном направлении и его аргумент в пределе стремится к p /2. Это означает, что пределом Z является комплексное индуктивное сопротивление.

При X(r) - µ , пределом вектора Z является бесконечно большое комплексное емкостное сопротивление.

Таким образом, изменение реактивного сопротивления в пределах - µ < X < + µ приводит к изменению угол сдвига фаз между током и напряжением в пределах - p /2 < j < + p /2.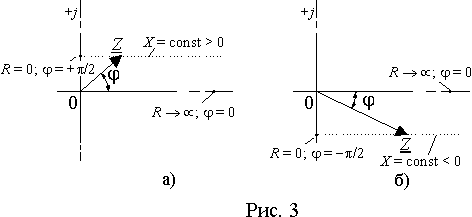

Рассматривая аналогичным образом вариации резистивного сопротивления R=var при постоянном положительном (рис. 3 а)) и отрицательном (рис. 3 б)) реактивном сопротивлении X , можно прийти к выводу, что в этом случае угол сдвига фаз между током и напряжением будет меняться соответственно в пределах +p /2 < j <0 и - p /2 < j < 0.

 ЗАДАЧА 2

Любой участок электрической цепи, имеющий только две точки подключения, называется двухполюсником. Через эти две точки в общем случае протекает электрический ток и существует некоторое падение напряжения. Если рассматриваемый участок электрической цепи не содержит источников электрической энергии, то такой двухполюсник называется пассивным. При наличии одного или более источников энергии в двухполюснике он называется активным.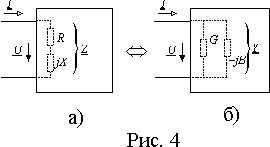

Если представить ток и напряжение на пассивном двухполюснике изображающими комплексными числами U и I (рис. 4), то их отношение будет комплексным сопротивлением Z или комплексной проводимостью Y и все рассмотренные выше соотношения будут справедливы по отношению к ним. Это означает, что в зависимости от параметров элементов образующих двухполюсник, их числа и схемы соединения, аргумент Z может находиться в пределах - p /2 < j < + p /2.

Предельными значениями для него будут углы j = - p /2, j = + p /2 и j = 0. Первые два значения соответствуют комплексным емкостному и индуктивному сопротивлениям. Фазовый сдвиг в 90° возможен только при условии, что внутри двухполюсника отсутствуют резистивные сопротивления. В дальнейшем будет показано, что в любой электрической цепи резистивная составляющая комплексного сопротивления связана с тепловыми потерями. Поэтому ее отсутствие означает отсутствие потерь энергии, что в нормальных условиях протекания электромагнитных процессов невозможно. Следовательно, невозможен и фазовый сдвиг между током и напряжением в 90° . Однако в реальных устройствах, в особенности в конденсаторах, потери могут быть столь незначительными, что ими можно пренебречь и считать двухполюсник чисто реактивным.

Рассмотренные закономерности позволяют представить любой сколь угодно сложный пассивный двухполюсник эквивалентным набором не более, чем двух элементов, который обеспечивает такую же связь между током и напряжением на входе, как исходный двухполюсник. Для этого достаточно знать модули тока и напряжения на входе и сдвиг фаз между ними. Все возможные варианты замещения двухполюсника приведены в таблице 1.

Таблица 1.

ЗАДАЧА 3 

В таблице 1 резистивно-индуктивный и резистивно-емкостной двухполюсники представлены двумя схемами - последовательной и параллельной. Они содержат реактивный элемент и резистор. Такому представлению соответствует учет потерь энергии в электромагнитных процессах, изображаемых на электрических схемах индуктивностью или емкостью.

Дело в том, что при любых электромагнитных процессах происходят необратимые потери энергии, связанные с преобразованием в тепло. Мощность этих потерь, в соответствии с законом Джоуля-Ленца, равна I²R или U²/R, где I и U - действующие значения тока и напряжения на участке электрической цепи, а R - его резистивное сопротивление. Однако резистивное сопротивление не обязательно должно быть сопротивлением проводника или проводящей среды. Сопротивлением можно представить даже процесс преобразования в тепло, не связанный в явном виде с протеканием электрического тока. Резистором можно также учесть механическую работу, совершаемую электромагнитными силами. При таких представлениях достаточно, чтобы соблюдалось равенство мощности выделяющейся в резисторе и в реальном процессе.

По соображениям удобства решения конкретной задачи, резистор можно подключить последовательно или параллельно реактивному элементу (L или C).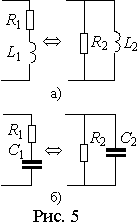

Тогда из выражений (9) соотношения между параметрами последовательной и параллельной схем замещения для рис. 5 а) будут

Из выражений (10) и (11) следует, что параметры элементов эквивалентных схем при взаимных преобразованиях зависят не только от параметров элементов исходной схемы, но и всегда от частоты.