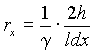 , где g - удельная проводимость материала магнитопровода. Тогда активная мощность, преобразуемая в тепло вихревыми токами PF , будет
, где g - удельная проводимость материала магнитопровода. Тогда активная мощность, преобразуемая в тепло вихревыми токами PF , будетДля увеличения индуктивности катушек их наматывают на замкнутые сердечники из ферромагнитного материала. В устройствах работающих на низких частотах для сердечников используют электротехническую сталь. При высоких частотах используются сердечники из спрессованного ферромагнитного порошка. Но независимо от конструкции и материала все катушки с ферромагнитным сердечником обладают рядом свойств и особенностей, которые мы рассмотрим. Для краткости в дальнейшем мы будем называть их просто катушками.
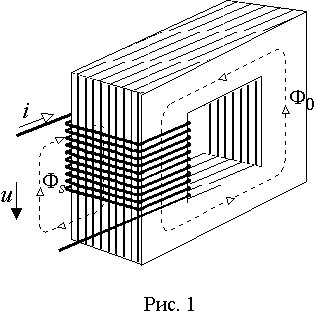
В основном катушки имеют конструкцию, показанную на рис. 1. На замкнутый сердечник из ферромагнитного материала различной формы и размеров наматываются проводники, по которым протекает переменный ток.
Протекающий ток создает вокруг катушки переменный магнитный поток, большая часть которого вследствие высокой магнитной проницаемости ферромагнетика замыкается по материалу Ф
0. Существенно меньшая часть магнитного потока охватывает витки катушки, замыкаясь по воздуху, и образует т.н. поток рассеяния Фs. Основной поток и поток рассеяния отличаются друг от друга не только количественно, но и принципиально. Поток рассеяния замыкается по среде, магнитная проницаемость которой не зависит от напряженности магнитного поля. Поэтому его величина линейно связана с величиной тока катушки. Основной поток замыкается по ферромагнетику, обладающему сильно выраженной нелинейной зависимостью магнитной проницаемости от напряженности поля и неоднозначной связью между ними. Все это делает невозможным общий точный анализ процессов в катушке и требует принятия допущений, позволяющих рассматривать катушку как объект с линейными характеристиками.Переменный магнитный поток, пронизывающий материал сердечника, вызывает появление в массе материала ЭДС индукции. Так как все ферромагнетики относятся к проводникам, то под действием этой ЭДС в сердечнике возникают электрические токи (
iF рис. 2), протекающие по замкнутым контурам, расположенным в плоскостях перпендикулярных направлению магнитного потока, и называемые вихревыми токами или токами Фуко.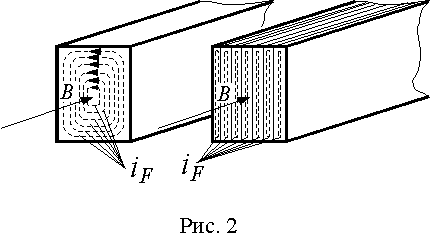
Вихревые токи
создают свой магнитный поток, стремящийся, в соответствии с правилом Ленца, ослабить изменение основного потока. Поэтому они действуют размагничивающим образом, уменьшая основной поток.Размагничивающее действие вихревых токов неодинаково в различных частях сердечника. Наиболее сильно оно выражено в центре сечения (рис. 2), т.к. центральные части охватываются максимальным числом контуров тока, МДС которых и создают размагничивающий поток. Поэтому в центре сечения плотность основного магнитного потока будет меньше, чем на краях, т.е. происходит вытеснение основного магнитного потока в наружные слои магнитопровода. Это явление выражено тем резче, чем выше частота магнитного потока и больше сечение, магнитная проницаемость и удельная проводимость материала сердечника.
Протекающий по материалу сердечника электрический ток вызывает его нагрев. Если это тепло не используется, то говорят о потерях на вихревые токи. В соответствии с законом Джоуля-Ленца, мощность расходуемая на нагрев равна IF2r, где IF - действующее значение вихревых токов, а r - сопротивление контура, по которому они замыкаются. Очевиднно, что эффективно снизить эти потери можно уменьшив ток. Это достигается увеличением удельного сопротивления материала и разделением его на отдельные изолированные друг от друга слои вдоль линий магнитного потока (рис. 2). Такое разделение на слои называется шихтованием магнитопровода.
Потери на вихревые токи можно определить, воспользовавшись понятием активной мощности переменного тока.
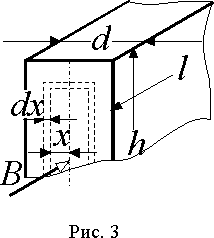
Пусть магнитопровод имеет форму параллелепипеда с длиной l, высотой h и толщиной d (рис. 3) и магнитный поток распространяется в направлении l. В плоскости перпендикулярной направлению вектора индукции B выделим элементарный замкнутый контур толщиной dx, стороны которого отстоят на расстоянии x от оси симметрии плоскости.
Если h >> d, то магнитный поток через поверхность, определяемую координатой x, будет Фx = 2xhB, а ЭДС, наводимая этим потоком в контуре dx - Ex = 4kf fФx max = 8kf fhxBm2, где kf - коэффициент формы ЭДС. Сопротивление контура dx , при условии, что сопротивлением меньших сторон (вдоль d) можно пренебречь, равно 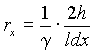 , где g - удельная проводимость материала магнитопровода. Тогда активная мощность, преобразуемая в тепло вихревыми токами PF , будет
, где g - удельная проводимость материала магнитопровода. Тогда активная мощность, преобразуемая в тепло вихревыми токами PF , будет
|
|
(1) |
Из выражения (1) следует, что потери на вихревые токи очень сильно (во второй степени) зависят от
Таким образом, уменьшение толщины листов пакета магнитопровода в два раза приведет к четырехкратному уменьшению потерь на вихревые токи.
Коэффициент
x является константой для конкретного магнитопровода, пропорциональной удельной проводимости материала и зависящей также от геометрической формы и размеров поперечного сечения.Кроме потерь на вихревые токи в сердечнике катушки существуют также потери, связанные с перемагничиванием материала в течение периода. В соответствии с формулой Штейнмеца, энергия теряемая на один полный цикл перемагничивания в единице объема вещества равна
WH` = h Bmn ,
где
h - постоянный коэффициент, характеризующий данное вещество, Bm - амплитуда индукции и n - показатель степени, зависящий от амплитуды индукции. Для значений индукции 0.1< Bm <1.0 Тл n = 1.6, а для 0.1 > Bm и 1.0< Bm <1.6 Тл n = 2.Отсюда мощность, расходуемая на перемагничивание или, иначе говоря, потери на гистерезис равны
|
PH = WH`fV = h fBmnV . |
(2) |
Общие потери в магнитопроводе
равны сумме потерь на вихревые токи и перемагничивание, т.е. PFe = PF + PH. Если принять, что потери на гистерезис пропорциональны второй степени Bm, то общие потери в магнитопроводе или, как говорят, "потери в железе" можно представить в виде|
PFe = (h f+x f2)Bm2V |
(3) |
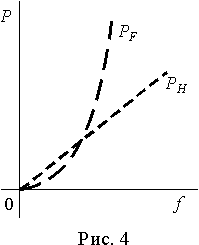
Зависимость потерь на вихревые токи
PF и гистерезис PH от частоты переменного тока представлена на рис. 4. При низких частотах в магнитопроводе преобладают потери на гистерезис, а затем, по мере роста частоты, потери на вихревые токи резко возрастают и при высоких частотах становятся преобладающими. При работе сердечника на высокой частоте оказывается невозможным его шихтование, т.к. невозможно изготовить пластины или ленту такой толщины, чтобы потери были удовлетворительными. Поэтому для высокочастотных сердечников шихтование заменяют прессовкой мелкодисперсных гранул ферромагнетика, размер которых можно выбрать таким, чтобы вихревые токи не превышали требуемых значений.Ферромагнитный материал сердечника катушки создает сильные искажения кривых тока и напряжения на ней. Гистерезисную петлю ферромагнетика
B(H) можно преобразовать в подобную ей зависимость потокосцепления катушки от тока Y (i), пользуясь тем, что Y = BS и i = H/w.Если катушка подключена к источнику синусоидальной ЭДС и напряжение на ней
u = Umcosw t, то потокосцепление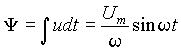 также синусоидальная функция времени. Построим кривую тока в катушке, пользуясь функцией Y (i) (рис. 5).
также синусоидальная функция времени. Построим кривую тока в катушке, пользуясь функцией Y (i) (рис. 5).
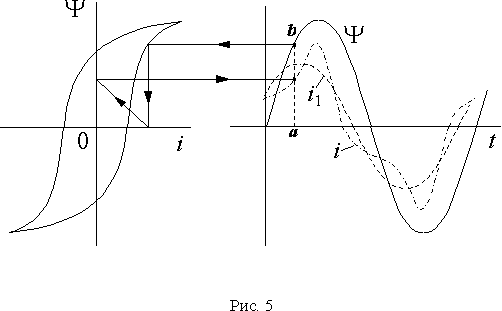
Для этого в каждый момент времени по значению
Y определим с помощью петли Y (i) мгновенное значение тока в катушке i и отложим его на вертикальной линии ab, соответствующей рассматриваемому моменту времени.Полученная кривая
i(t) имеет сильные искажения. В ее спектре резко выражена третья гармоника. Если выделить первую гармонику i1 (рис. 5) , то окажется, что синусоида потокосцепления отстает от нее на некоторый угол, называемый гистерезисным углом. Величина гистерезисного угла зависит от ширины петли гистерезиса, т.е. от потерь на перемагничивание. Если петлю гистерезиса заменить кривой намагничивания, то искажения кривой тока сохранятся, а гистерезисный угол будет равен нулю.Если катушку подключить к источнику синусоидального тока
i, то по петле i(Y ) можно также по точкам для каждого момента времени построить кривую Y (t), а затем, продифференцировав ее, получить кривую u(t) (рис. 6).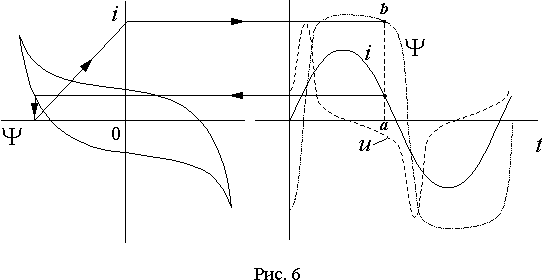
Из рис. 6 следует, что при синусоидальном токе в катушке кривая падения напряжения на ней несинусоидальна и имеет ярко выраженную третью гармонику. Причем ее доля в спектре напряжения существенно больше, чем в спектре тока при синусоидальном напряжении.
При анализе электрических цепей с несинусоидальными токами и напряжениями их заменяют эквивалентными синусоидами, имеющими такое же действующее значение. Найдем связь между потокосцеплением катушки и протекающим в ней током при условии, что все функции синусоидальны, т.е.
u = Umcosw t; Y = Y msinw t; i = Imcos(w t- j ) .
Ток
i отстает от падения напряжения на катушке u на некоторый угол j , определяемый из равенства cosj =PFe/(UI), а напряжение и потокосцепление находятся в квадратуре, т.к. u = dY /dt.Из выражения для тока
i - Imsinw tsinj = Imcosw tcosj .
Следовательно
i2 - 2iImsinw tsinj + Im2sin2w tsin2j = Im2cos2w tcos2j
и, прибавляя к обеим частям
Im2sin2w tcos2j , с учетом того, что sinw t = Y / Y m, получим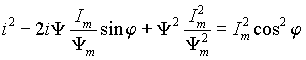 .
.
Это выражение является уравнением эллипса с центром в начале координат. Таким образом, замена несинусоидальных кривых тока и напряжения означает замену истинной петли функции
Y (i) эквивалентным эллипсом, площадь которого пропорциональна потерям энергии в магнитопроводе за один период.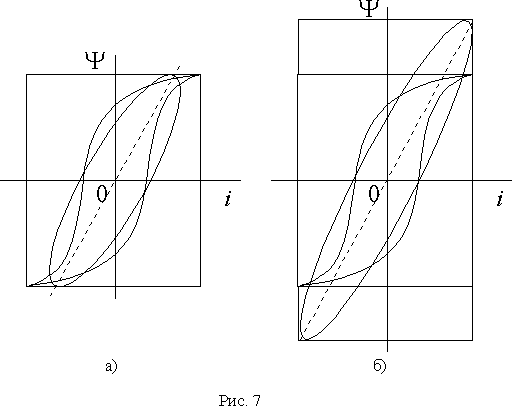
Эллипсы функции
Y (i) при замене несинусоидального тока и напряжения катушки приведены соответственно на рис. 7 а) и б).Если сердечник катушки заменить проводящим неферромагнитным материалом, то в нем исчезнут потери на гистерезис, но останутся вихревые токи и связанные с ними потери. Кривые напряжения и тока в катушке при этом будут синусоидальными, а смещение их по фазе
j будет соответствовать величине потерь. Зависимость Y (i) в этом случае будет иметь форму эллипса. Следовательно, при наличии потерь на гистерезис графическая форма функции Y (i) представляет собой нечто среднее между эллипсом и гистерезисной петлей. При уменьшении частоты доля потерь на вихревые токи уменьшается и форма Y (i) приближается к гистерезисной петле. При увеличении частоты потери на вихревые токи быстро растут и форма петли Y (i) становится близкой к эллиптической.После замены кривых напряжения и тока в катушке с ферромагнитным сердечником эквивалентными синусоидами можно построить для нее векторную диаграмму и соответствующую схему замещения.
Пусть магнитный поток в сердечнике катушки изменяется по закону Ф =Ф
msinw t, тогда наводимая этим потоком в катушке ЭДС e = - dФ/dt будет отставать от него на 90° , а падение напряжения в катушке u0 = - e - опережать поток Ф на такой же угол. При отсутствии потерь в магнитопроводе ток катушки имел бы только реактивную составляющую Iр и совпадал бы по фазе с магнитным потоком. Катушка в этом случае обладала бы только реактивным сопротивлением x0 = U0/Iр или индуктивностью L0 = x0/w (рис. 8 а)).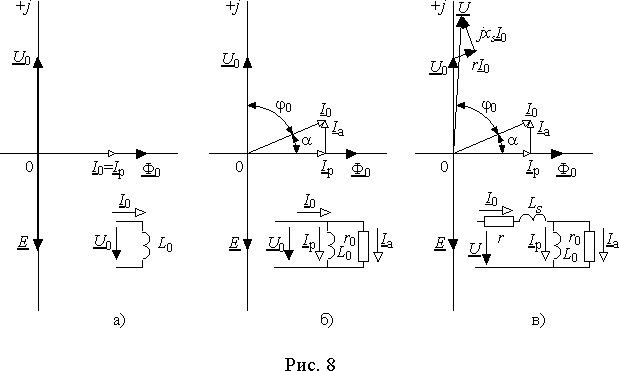
При наличии потерь на гистерезис и вихревые токи ток катушки будет иметь также активную составляющую
Iр, опережающую по фазе реактивную на 90° . Ее значение и соответствующее резистивное сопротивление можно определить из мощности потерь в магнитопроводе - Iа = PFe/U0 ; r = U0/Iа . При этом ток катушки будет отставать от напряжения на угол j , который можно определить изcosj = sina = PFe/(U0I0) ,
где a
= p /2- j , т.н. угол магнитного запаздывания. Так как угол магнитного запаздывания обычно мал, то в выражениях для x0 и L0 реактивную составляющую тока можно заменить на I0 без существенной погрешности. Векторная диаграмма и схема замещения катушки с учетом потерь в сердечнике приведена на рис. 8 б).Проводники катушки обладают конечным значением сопротивления
r и протекающий по ним ток вызывает тепловые потери. Часть магнитного потока замыкается по воздуху, минуя сердечник, и создает т.н. поток рассеяния Фs, который создает в катушке ЭДС самоиндукции. Учесть эти явления в векторной диаграмме и схеме замещения можно, дополнив их соответствующими элементами.На резистивном сопротивлении катушки
r возникает падение напряжения ur = ri0, совпадающее по фазе с током i0. Падение напряжения вызванное ЭДС самоиндукции uLs = Lsdi/dt Û ULs = jxsI0 опережает ток i0 на 90° , и может быть изображено на электрической схеме соответствующим индуктивным сопротивлением xs или индуктивностью Ls. При этом напряжение на катушке кроме ЭДС, создаваемой основным магнитным потоком, должно уравновешивать также ЭДС самоиндукции, создаваемую потоком рассеяния, и падение напряжения на резистивном сопротивлении.Векторная диаграмма для случая полного учета потерь в катушке с ферромагнитным сердечником и потока рассеяния и соответствующая ей схема замещения приведены на рис. 8 в). Резистивное сопротивление
r учитывает тепловые потери в обмотке катушки, а r0 - потери в магнитопроводе. Индуктивность Ls соответствует потоку рассеяния катушки Фs, а индуктивность L0 - основному магнитному потоку Ф0.Следует заметить, что на рис. 8
величина угла a и размеры векторов rI0 и jxsI0 для наглядности существенно увеличены, т.к. в действительности они составляют несколько процентов от напряжения U.