Любое неотрицательное число в позиционной системе счисления (СС) может быть представлено в виде:
D = Cn-1*bn-1 + Cn-2*bn-2 + ... + C1*b1
+ C0*b0 + C-1*b-1 + C-2*b-2
+..,
где D - десятичный эквивалент числа, Ci - значение i-го разряда, b - основание системы счисления,b в степени i - вес i-го разряда и n число разрядов целой части числа. В вычислительной технике ниболее распространены: двоичная (BIN), десятичная (DEC), шестнадцатиричная (HEX) и непозиционная двоично-десятичная (BCD) системы счисления. В BCD системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая цифра i-го разряда кодируется 4-мя двоичными цифрами. Восьмиричная СС (OCT) применяется реже. Первые 16 чисел представлены в таблице 1.
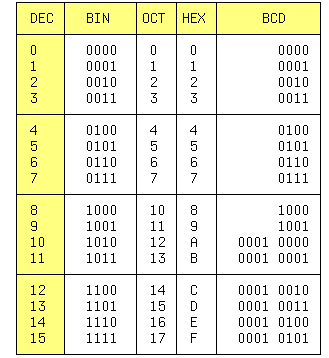
Двоичное число 10010011 = 1 * 2^7 + 1 * 2^4 + 1 * 2^1 + 1 * 2^0 = 147 (DEC). Для перевода числа из двоичной системы в 16 - ную, его необходимо разбить начиная справа на группы по 4 двоичных цифры и каждую группу представить 16 - ной цифрой из таблицы. Для обратного перевода каждая HEX цифра заменяется четверкой двоичных, незначащие нули слева отб- расываются. Двоично-десятичное число можно записывать и десятичными цифрами, например 1997, и двоичными - 0001 1001 1001 0111. Каждое десятичное число можно представить в виде BCD, например 19(DEC) = 19(BCD), но их двоичные представления не равны: 19(DEC) = 10011(BIN), а 19(BCD) = 1 1001(BIN). Не каждая запись из нулей и единиц имеет двоично-десятичный эквивалент. Например, 11001001(BIN) = ?(BCD) = C9(HEX) = 201(DEC), т.к. десятичной цифры 12 = 1100 несуществует!
Микропроцессоры обрабатывают упорядоченные двоичные наборы. Минимальной единицей информации является один бит.

Далее следуют - тетрада (4 бита), байт ( byte 8 бит), двойное слово (DoubleWord 16 бит) или длинное (LongWord 16 бит) и учетверенное слова. Младший бит обычно занимает крайнюю правую позицию.
Такие числа могут быть как целыми, так и дробными. Точка мысленно фиксируется рядом с любым разрядом. Если она располагается справа от младшего бита, то число целое, если слева от старшего - число дробное. Далее будут рассматриваться только целые числа с фиксированной точкой, для нецелых чисел чаще применяется показательная форма, о которой пойдет речь дальше.
Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит - знаковый. Отрицательному числу соответствует единичный бит, а положительному - нулевой. Каждый способ оценивается по скорости и затратам на выполнение сложения и изменения знака числа, т.к. вычитание есть сложение с измененным знаком одного операнда.
00000111 = 7
11111010 =-5 (инверсия 00000101 = 5)
1 00000001
1
00000010 = 2
Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0...00 равна 1. ..11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11.Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно почему код называется дополнительным "до 1". Этих недостатков лишен ---
00001001 = 9 11110111 =-9
11110110 - инверсия 00001000 - инверсия
1 1
11110111 =-9 00001001 = 9
Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.
00001001 = 9 11110111 =-9 1 00000000
Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный "до 2-х" код.
7.4 ДИАПАЗОН ЦЕЛЫХ ЧИСЕЛ С ФИКСИРОВАННОЙ ТОЧКОЙ
Беззнаковые числа: 0 <= D <= 2^n - 1. n - число разрядов
Байт: 0 - 255 (DEC) Слово: 0 - 65535
00..0 - 11..1 (BIN) 00..0 - 11..1
0 - FF (HEX) 0 - FFFF
Числа со знаком:-2^(n-1) <= D <= +2^(n-1)-1. n - число
разрядов.
Байт: -128 - +127 (DEC) Слово: -32768-+32767
10..0 - 01..1 (BIN) 10..0 - 01..1
80 - 7F (HEX) 8000 - 7FFF
Вещественные числа хранятся и используются в ЭВМ в показательной форме, т.е. в виде двух составляющих: мантиссы и порядка. Различия в способах такого представления чисел заключаются в количестве байтов отводимых под порядок и мантиссу и небольших отличиях в форме их хранения. Например в четырехбайтовом формате под мантиссу отводится 3 байта и один байт для хранения порядка (КВ - короткий вещественный формат).
D = ±M * 2^(E-127)
Последовательность расположения байтов

в различных ЭВМ может быть разной. D - десятичный эквивалент числа , M - нормализованная мантисса, Е - смещенный порядок, SM - бит знака мантиссы.
У нормализованной мантиссы первая значащая цифра (единица) мысленно находится слева от запятой, а справа располагаются 23 разряда - 1,xx..xx. Поэтому Mmax = 1,111..11 = 1 +1/2 +1/4+ 1/8 +...= 2, а Mmin= 1,000..00 = 1 для положительных чисел (SM=0) и -1 и -2 для отрицательных, (SM=1). Порядок числа Emax = 11111110 = 254, а Emin = 00000001 = 1. Теперь нетрудно определить диапазон представления положительных чисел от +Dmax = Mmax * 2^(254-127) = 3,4 * 10^38 до +Dmin = Mmin * 2^(1-127) = 1,17 * 10^(-38). Точность определяется числом достоверных десятичных цифр. При 23 двоичных разрядах мантиссы 2^23 примерно равно 10^7, т.е. достоверными являются только 6-7 значащих десятичных знаков, а не 38. Необходимо отметить, что значения порядка 11111111 и 00000000 по международному стандарту IEEE 754 и 854 предназначены для кодирования денормализованных чисел, отрицательной и положительной бесконечностей, неопределенности и, так называемых Не-чисел.
Двоично-десятичный код (ДДК) или Binary Coded Decimal (BCD) может быть упакованным, когда в одном байте хранятся две десятичные цифры, либо неупакованным - по одной цифре в байте.Упакованное число 1996 представляется в виде двух байтов: 0001 1001 и 1001 0110. Для знака числа отводится дополнительный байт, например в формате (ДД) девять байтов отводится для размещения 18-ти цифр, а в старшем бите десятого байта находится знак числа.
Для вывода информации на устройства отображения, например дисплей или принтер, а также для ввода или передачи данных используются буквенно-цифровые коды. Буквы, цифры, математические символы, знаки препинания, символы для рисования линий, управляющие символы и некоторые другие кодируются однобайтовыми числами. Существует несколько разновидностей таких кодов, например: ASCII, КОИ-7, КОИ-8, альтернативный код ГОСТ, основной код ГОСТ и другие. ASCII и 7-ми битовый код для обмена информацией (КОИ-7) отображают первые 128 символов и входят в состав остальных кодировок. Дополнительные символы и русский алфавит входят в восьмибитовые расширенные коды (КОИ-8, альтернативный и основной). Общее число символов в этих кодах равно 256. Таблица некоторых кодов приведена ниже. Следует отметить, что нулевой код (NULL) не кодирует цифру ноль и вообще никак не отображается.
Символ ¦ Код(HEX) Символ ¦ Код(HEX) Символ ¦ Код(HEX) --------+--------- -------+--------- -------+--------- "ничего"¦ 00 "A" ¦ 41 "А" ¦ 81 "0" ¦ 30 "B" ¦ 42 "Б" ¦ 82 "1" ¦ 31 "C" ¦ 43 "В" ¦ 83 .. ¦ .. .. ¦ .. .. ¦ .. "9" ¦ 39 "Z" ¦ 5A "Я" ¦ 9F ":" ¦ 3A "[" ¦ 5B "а" ¦ A0 \_________ASCII кодировка___________/ \_______________альтернативная кодировка_______________/
В Internet для русского языка используется кодировка КОИ-8. В настоящее время разработан и используется 16-ти битовый Unicode с 65536 различными симвоволами.
Служит для отображения образа BCD или HEX цифры высвечиваемой на индикаторе в виде набора 0 и 1. Может быть принято следующее соответствие между битами и сегментами:
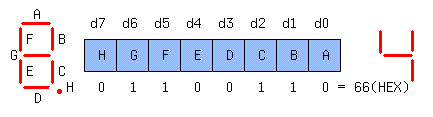
Внизу приведен битовый набор для высвечивания цифры 4. Единицы обычно соответствуют светящимся сегментам.
Набор единиц и нулей хранящихся в регистре или ячейке памяти (двоичный набор) для микропроцессора ничего не означает. Пусть в регистре находится набор из восьми битов 10000110. Он может быть интерпретирован следующим образом, как:
1) двоичное число = 10000110, имеющее
а) шестнадцатиричный эквивалент = 86(HEX),
б) восьмиричный эквивалент = 206(OCT),
в) десятичный эквивалент числа без знака = 134(DEC),
2) дополнительный код отрицательного числа =-122(DEC),
3) двоично-десятичное упакованное число = 86(BCD),
4) альтернативный код буквы "Ж",
4') код КОИ-8 символа "¦",
5) восьмисегментный код цифры "1.",
6) часть вещественного числа,
7) реализация множества,включающего 3 элемента из 8-ми,
8) часть адреса ячейки памяти или внешнего устройства,
9) код операции и т.д.
Поэтому ответственность за интерпретацию двоичных наборов возлагается на программиста. Например, попытка сложить ASCII коды "1" + "2" не даст в сумме код "3", а даст 31(HEX) + 32(HEX) = 63(HEX), что соответствует коду латинской буквы "c".