1. Обобщенная функция Хевисайда -это функционал, действующий следующим образом

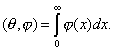
Он порожден локально-интегрируемой функцией Хевисайда:
.

Найдем производную от обобщенной функции .

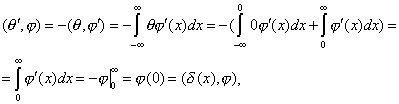
то есть

2. Производная от - функции есть функционал, действующий по формуле

n-ая производная от -функции есть функционал, действующий по формуле

3. Докажем, что .

Доказательство

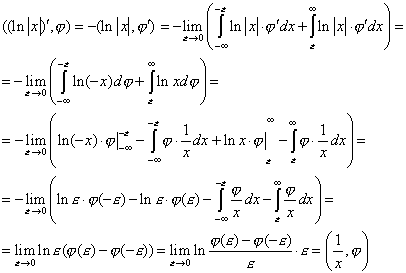
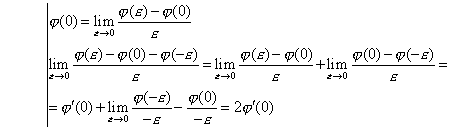
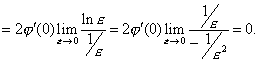
Доказано.

4. Проверим, что произведение бесконечно дифференцируемой функции х на обобщенную функцию есть обобщенная функция 1

.

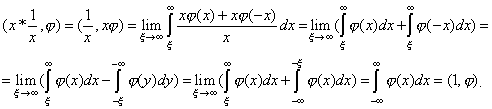
Доказано.

Часто рассматривают дифференциальные уравнения с обобщенными функциями. Чтобы пояснить характер работы с обобщенными функциями, проверим, что обобщенные функции являются решениями уравнения

.

(2)

Сначала решим это уравнение в обычных функциях.

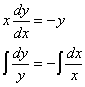
-обычное решение дифференциального уравнения.
Докажем, что обычное решение является так же и обобщенным решением. Кроме того, обобщенная функция тоже является решением этого дифференциального уравнения.

Доказатнльство

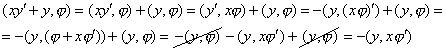
Полагая y равной и , получаем

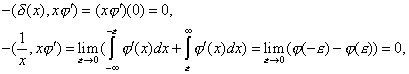
следовательно, и -это решения уравнения (2).

Доказано.