3.3 Интерференция в диффузном свете. Опыт Берча-Токарского

Интерференция в диффузном свете

Плоскопараллельная пластинка L освещается пучком параллельных лучей. Поверхность AB пластинки - диффузно отражающая, а ее задняя поверхность - зеркальная. Рассмотрим ход лучей по двум разным оптическим путям (рис. 35).

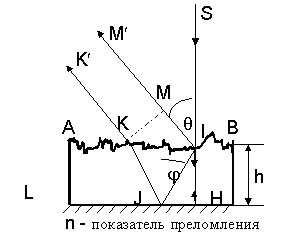
Рис. 35 Интерференция на бесконечности лучей, рассеянных в точке I

1) Падающий луч SI нормально входит в толщу пластинки в точке I, идет вдоль пути IHI и в той же точке I диффузно рассеивается во всех направлениях. Рассмотрим, например, направление IM¢, составляющее угол q с нормалью к пластинке.

2) Падающий луч SI в точке I диффузно рассеивается во всех направлениях. Рассмотрим, например, направление IJ, такое, что луч, распространяющийся вдоль него, испытывает в точке J зеркальное отражение и далее идет в направлении KK¢, параллельном MM¢.

Диффузное рассеяние света, обусловленное частицами шероховатой поверхности, приводит к беспорядочному изменению фаз падающих лучей. Два луча, диффузно рассеянных поверхностью AB, могут интерферировать даже в случае, даже если они рассеиваются двумя разными точками поверхности. При переходе от одной пары лучей к другой разность фаз меняется беспорядочно и для всего светового пучка интерференционная картина будет отсутствовать. Но для лучей, диффузно рассеянных одной и той же точкой, это не так: два луча, такие как SIHIM¢ и SIJKK¢, рассеянные одной и той же точкой I поверхности AB, способны интерферировать. Это справедливо для любой точки поверхности AB и, следовательно, для всей совокупности лучей светового пучка.

Вычислим разность хода D между двумя рассмотренными выше лучами SIHIM¢ и SIJKK¢.

,

n - показатель преломления пластинки L . Если углы q и j малы, то

Лучи SIHIM¢ и SIJKK¢ на выходе из пластинки L идут в параллельных направлениях и интерферируют на бесконечности. Интерференционные полосы можно наблюдать в следующей оптической схеме(рис. 36).

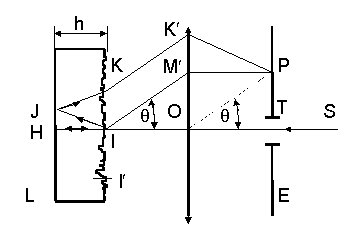
Рис. 36 Образование интерференционных колец в плоскости экрана Е

В фокальной плоскости линзы O помещен экран E, в котором имеется малое отверстие T, через которое проходит узкий пучок излучения. Падающий луч SI испытывает диффузное рассеяние в точке I либо до, либо после отражения на задней поверхности пластинки L. Интерферировать будут лучи IHIM¢ и IJKK¢, испытавшие диффузное рассеяние в одной и той же точке I поверхности AB. Выйдя из пластинки, эти два луча распространяются в параллельных направлениях KK¢ и IM¢ и интерферируют в точке P фокальной плоскости линзы O. Их разность хода определяется выражениями, аналогичными предыдущему случаю. Интенсивность в точке P, обусловленная интерференцией этих лучей, дается классической формулой Френеля. Полагая, что амплитуды одинаковы, получим для интенсивности

Для другой точки I¢ поверхности AB фаза интерферирующих волн будет иной, поскольку фазы волн, диффузно рассеиваемых разными точками поверхности AB, изменяется беспорядочно. В силу симметрии, рассматриваемой схемы и диффузного характера рассеяния падающего излучения на окружности, соответствующей точке P интенсивность излучения будет одинакова. Следовательно, интерференционная картина будет иметь круговую симметрию и представлять систему колец (рис. 37).

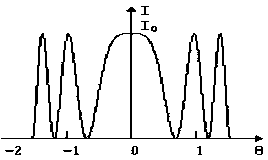
Рис. 37 Распределение интенсивности в интерференционных кольцах

В направлении q, т.е. в точке P фокальной плоскости E линзы O, будет наблюдаться светлое кольцо, если

,

где p - целое число. Угловой радиус первого светлого кольца будет (p=1)

.

В случае стеклянной пластинки толщиной 0,5 мм с показателем преломления n=1,5 первое светлое кольцо имеет угловой диаметр 2q, в 8 раз превышающий угловой диаметр Солнца (при фокусном расстоянии 50 мм диаметр первого светлого кольца равен 4,35 мм; l= 0,63 мкм; q=0,043;).

Существуют различия между этими кольцами и кольцами, наблюдаемыми в интерферометре Майкельсона, локализованными на бесконечности. Для колец, возникающих в диффузном свете, порядок интерференции в центре (q=0) всегда равен нулю независимо от толщины h пластинки, т.е. яркое светлое пятно будет совпадать с отверстием T. На следующем рисунке представлена кривая зависимости интенсивности I от угла q. Толщина диффузной пластинки h влияет только на диаметр колец. В интерферометре же Майкельсона интенсивность в центре зависит от «толщины» пластинки, и поэтому в белом свете кольца кажутся окрашенными и наблюдается только при условии, что разность хода D очень мала. Кольца же, наблюдаемые в при диффузном рассеянии, всегда видимы и в белом свете, независимо от толщины h. В центре этих колец всегда располагается светлое пятно.

Опыт Берча-Токарского

Наличие зашумляющей изображение спекловой структуры является недостатком многих систем когерентной оптики. Однако спеклы нашли и полезное применение. Это обработка оптических изображений, регистрация смещений и деформаций диффузных объектов, астрономические исследования, связанные с изучением двойных звезд и измерением видимого диаметра звезды по пространственному спектру, создаваемому ею в присутствии атмосферной турбулентности спекл-структуры, измерение шероховатости и т.п.

Многие из этих применений связаны с обнаруженной в опыте Берча и Токарского возможностью введения в оптику пространственной несущей частоты и связанной с ней техники фильтрации изображений.

Рассмотрим следующую схему (рис. 38).

Рис. 38 Схема регистрации спекл-картины на фотопластинке Н

Матовое стекло G освещают лазером и регистрируют спекл-структуру на фотопластинке. Спекл-структура в плоскости H характеризуется функцией D(x,h), описывающей распределение интенсивности света в этой плоскости. После проявления на кривой пропускания t фотопластинки имеется линейный участок AB (рис. 39):

Рис. 39 Амплитудное пропускание негатива

Эту область и стараются использовать. В этой области амплитуда t и интенсивность D(x,h) связаны линейным соотношением.

Будем считать, что интенсивность D(x,h) такова, что амплитудное пропускание проявленного негатива не выходит из области линейности. Тогда амплитудное пропускание негатива можно записать

t = a - bD(x,h),

где a, b - константы, зависящие от свойств используемой фотоэмульсии.

Сделаем теперь не одну, а две одинаковые по времени экспозиции, сместив в промежутке фотопластинку. Регистрируемая интенсивность будет

D( x , h ) + D( x-x₀ , h )

Так как смещение эквивалентно свертке с дельта-функцией, регистрируемую интенсивность можно записать в виде

Таким образом, если на фотопластинке высокого разрешения зарегистрировать два изображения одной и той же спекловой структуры (например от матового стекла) со сдвигом в пространстве на x, то получится негатив с амплитудным коэффициентом пропускания вида

где D(x,h ) - распределение интенсивности в спекловой структуре;

Пространственный спектр зарегистрированной картины будет иметь вид

где - Фурье -образ функции, а u,v - угловые координаты в фокальной плоскости.

При освещении негатива параллельным пучком лучей в фокальной плоскости линзы О можно получить изображение этого спектра. Член ad(u,v) соответствует (если пренебречь дифракцией) изображению точечного источника, расположенного на бесконечности. Это изображение локализовано в фокусе F. Второй член представляет собой (умноженный на константу b) Фурье -образ функции D(u,v), модулированный функцией Диффузор D(u,v) имеет очень тонкую структуру, а поэтому его Фурье образ сильно растягивается в фокальной плоскости линзы О (рис. 40).

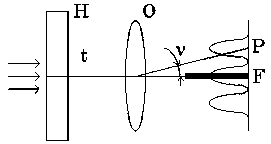
Рис. 40 Спектр двух идентичных смещенных относительно друг друга спекл-структур

Фурье-образ , как и сама функция D(u,v) тоже описывает некую спекл -структуру. Если пренебречь изображением источника в фокусе F, то во всей остальной части фокальной плоскости интенсивность света с точностью до постоянного множителя будет равна.

Таким образом, диффузный фон ïïоказывается модулированным функцией cos²(pux₀/l), описывающей полосы Юнга. Угловое расстояние между двумя соседними полосами равно l / x₀. Например, при смещении на 20 мкм угловое расстояние между двумя светлыми полосами составляет 1⁰ 42¢ .

Спекл-структура на негативе H состоит из мелких темных пятен, и, согласно теореме Бабине, ее спектр (всюду, кроме точки F) имеет тот же вид, что и спектр дополнительного непрозрачного экрана с малыми отверстиями на местах темных пятен. В рассмотренном выше мысленном опыте времена обеих экспозиций одинаковы и контраст полос Юнга максимален: т.е. минимальная интенсивность темных полос равна нулю.

Несколько экспозиций на одной фотопластинке

Сделаем ряд экспозиций с одинаковыми временами и одинаковыми смещениями фотопластинки (в одном и том же направлении) в промежутке между экспозициями. Если число экспозиций равно N + 1, то регистрируемая интенсивность будет равна свертке

Если осветить негатив, то в произвольной точке (u,v) фокальной плоскости линзы О амплитуда будет определяться Фурье-образом. Если не учитывать изображения источника в фокусе F, то, с точностью до постоянного множителя для интенсивности, будем иметь выражение

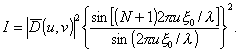
Спектр, наблюдаемый в фокальной плоскости линзы О, будет таким же, как и спектр дифракционной решетки с периодом x₀ и числом штрихов N + 1. Между двумя главными максимумами располагается N-1 вторичных максимумов.

Рис. 41 Спектр для случая нескольких экспозиций со смещением

Если число экспозиций N + 1 достаточно велико, то можно представить регистрируемую интенсивность в виде

,

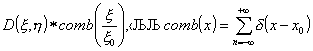- гребенчатая функция.

Откуда для спектра интенсивности в фокальной плоскости линзы О получим

Вычитание изображений

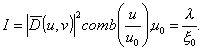
Задача: на двух диапозитивах A и B наряду с одинаковыми имеются и неодинаковые участки, и нужно получить разность (A - B). Диапозитивы A и B могут представлять собой, например, полученные в разное время две фотографии одного и того же участка земной поверхности, на котором произошли какие - то изменения в промежутке между съемками. Требуется выявить эти изменения.

С этой целью делают копии диапозитивов A и B на одной и той же фотопластинке H высокого разрешения. При первой экспозиции перед H помещают диапозитив A и освещают его спекл -структурой, создаваемой матовым стеклом G, затем A заменяют B, и прежде чем сделать вторую экспозицию, смещают H на некоторое расстояние. При смещении H на ней запечатлеваются две спекл-структуры смещенные на малое расстояние. На одинаковых участках диапозитивов A и B имеются пары идентичных пятен. При дифракции два идентичных пятна дают интерференционные полосы Юнга в фокальной плоскости объектива. Поместим в фокальную плоскость непрозрачный экран со щелью таким образом, чтобы щель совпала с темной полосой, тогда свет, дифрагированный двумя пятнами, не будет попадать на плоскость изображения, что справедливо и для всех пар одинаковых пятен. Это означает, что, все одинаковые участки диапозитивов A и B не будут видны на изображении H¢.

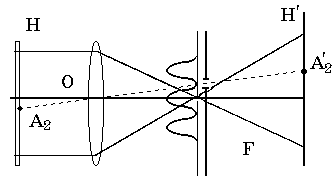
Рис. 42 Выявление в плоскости Н разницы двух изображений

В тех участках, где диапозитивы A и B не одинаковы, они дадут при дифракции на фотопластинке H полосы неодинаковой интенсивности (интенсивность в минимумах не будет равна нулю). И, в результате, в плоскости H¢ будут видны те участки изображений, на которых есть различия, т.е. видна "разность" изображений (A - B).

Регистрируя диапозитивы на фотопластинке по описанной схеме, получают негатив с пространственным спектром:

Спектр содержит три составляющие, из которых только одна несет полезную информацию. Две другие должны быть отфильтрованы в процессе восстановления. Это достигается помещением в фокальную плоскость линзы экрана со щелью, приходящейся на минимум интерференционных полос, описываемых множителем . Экран пропускает только составляющую

В плоскости изображения H¢ будет видна картина , промодулированная спекл-структурой D. Такая структура спеклов мало сказывается на качество изображения С, поэтому можно считать задачу решенной.

---