Уровень: Основной текст Подробнее Глоссарии: ... Глоссарий

Концепция универсального эволюционизма

Составим простейшую математическую модель процесса эволюции. Рассмотрим системы, в которых изменение во времени некоторого параметра = пропорционально величине этого параметра, т. е. ~q. Такие системы носят название автокаталиктических. В качестве параметра q могут фигурировать концентрация, температура, число людей на планете и т. д. Простейшее эволюционное уравнение примет вид

= q,

Решение этого уравнения:

q=q₀ е ,

Параметр может быть положительной, отрицательной, мнимой величиной, что определяет характер эволюции. Например, при > 0 процесс идет в направлении возрастания q по закону экспоненты, при < 0 - по закону убывания по экспоненте, при = iа - процесс подчиняется гармоническому закону, а для комплексного значения параметра = b+iа возникает эволюция при комбинации экспоненциального и комплексного законов (рис. 1).

Рис 1. Зависимость параметра q от для разных типов .

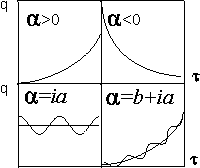
Как ранее указывалось, синергетическим системам свойственна стохастичность, т. е. их временную зависимость нельзя предсказать с абсолютной точностью. Поэтому для таких систем вводят в уравнение член f( ), учитывающий флуктуации в системе, т. е.

= q+f( ).

Рассмотрим более сложный случай: вещество 1 с концентрацией q₁ образуется автокаталитически ( ~q) в результате взаимодействия с веществом 2, концентрация которого q₂, тогда

С учетом стохастичности синергетической системы эволюционное уравнение примет вид

.

С помощью последнего уравнения можно описать различные типы поведения популяции. В этом уравнении b описывает характер связи между параметрами q₁ и q₂ и, если он регулируется извне, то b играет роль управляющего параметра.

В реальных синергетических системах много подсистем q₁, q₂,..., q_n, и при составлении математической модели важно выделить уровни описания: микроскопический (атомы, молекулы), мезоскопический (ансамбль атомов и молекул), макроскопический (протяженные области из атомов и молекул и их ансамблей). Например, при описании роста кристаллов эволюционные уравнения содержат параметры q₁(х, ) - плотность вещества в жидкой и q₂(х, ) - в твердой фазе. Из уравнений можно определить образование во времени твердой фазы q₂( ) в зависимости от плотности в жидкой фазе q₁(х, ), т. е. q₂( )= f(q₁, ).

Численность популяций. Рассмотрим сначала динамику популяций, т. е. какие факторы контролируют численность популяций, как много различных популяций могут сосуществовать. Начнем с какой-либо одной популяции (бактерии, растения, животные данного вида). Основная характеристика - число особей n в популяции. Оно меняется в зависимости от скорости рождения (числа рождений) g и от скорости гибели (числа смертей) d:

=g-d

Скорости рождения и смерти зависят от числа имеющихся особей

g = n, d = n,

где коэффициенты и не зависят от n, т. е. рост не зависит от плотности популяции. Но они зависят от таких параметров, как количество доступной пищи, температура, климат и т. д. При постоянном значении этих факторов

= n =( - )

Это уравнение описывает либо экспоненциально растущую, либо экспоненциально убывающую популяцию, но стационарное состояние =0 невозможно, и для существования процесса следует допустить, что коэффициенты и должны зависеть от плотности. Причина последнего также связана с ограничениями в пище. Если учесть истощение источников питания, то, как было показано выше, перейдем к уравнению Ферхюльста

= ₀- n²

Это уравнение обладает значительной самостоятельной ценностью, поэтому настоятельно рекомендуем ВСЕМ прочитать посвещенный ему параграф.

Модели конкуренции и сосуществования. Если различные виды не питаются одной и той же пищей и не взаимодействуют друг с другом, они могут сосуществовать. Уравнения для численности видов j записываются в виде

_j = _j - _j n_j², j = 1, 2, ...

Ситуация осложняется, если различные виды живут за счет одного и того же источника пищи, и они зависят от одних и тех же условий жизни.

Пусть n₁ и n₂ численности особей двух видов, которые питаются из одного и того же источника пищи N₀. При таком условии выживает только один вид, а другой вымирает, т. к. вид с большей константой размножения поедает пищу гораздо быстрее, чем другой вид. Отметим, что количество пищи не задается в начальный момент, а поступает постоянно с определенной скоростью.

Чтобы популяция выжила, важно улучшить ее индивидуальные константы _j и _j путем адаптации, а также важно дополнительное поступление пищи. Рассмотрим два вида 1 и 2, живущие за счет "перекрывающихся" источников питания. Эту ситуацию можно промоделировать уравнениями

= ( ₁₁N₁ + ₁₂N₂)*n₁- ₁n₁

= ( ₂₁N₁ + ₂₂N₂)*n₂- ₂n₂

Модель хищник - жертва. Эта модель носит в литературе название модели Лотки-Вольтера. Рассмотрим существование в море рыб двух типов - рыб-хищников и рыб-жертв. Скорость изменения популяций j=1, 2 дано уравнением

₁= Прирост _j - Потери _j, j =1, 2.

Обозначим рыб-жертв индексом 1. Если хищников нет, то рыбы-жертвы размножаются по закону

Прирост ₁ = ₁ n₁.

Но рыбы-жертвы поедаются хищниками и число рыб-жертв уменьшается, а потери пропорциональны числу жертв n₁ и хищников n₂

Потери ₁ = n₁ n₂.

Рассмотрим теперь уравнение для j = 2 (рыб-хищников). Поскольку хищники живут за счет жертв, скорость размножения хищников пропорциональна их собственному числу и числу жертв

Прирост ₂ = n₁ n₂,

Потери ₂ = 2 ₂ n₂.

Итак, уравнения модели Лотки-Вольтера имеют вид

= ₁n₁ + n₁n₂

= n₁n₂- 2 ₂ n₂

Эти уравнения можно привести к безразмерному виду

,

,

Если положить

, , .

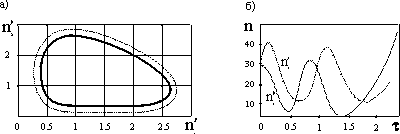
На рис. 2а представлены две типичные траектории на плоскости (n₁', n₂') в модели Лотки-Вольтера при фиксированных параметрах. Из этого рисунка следует, что изменение n₁ и n₂ периодично (рис. 2б): когда хищники размножаются слишком сильно, то и жертвы уничтожаются ими очень быстро. Поэтому запасы пищи у хищников уменьшаются и соответственно уменьшается численность хищников. В результате число животных-жертв увеличивается, т. е. растут запасы пищи у хищников, которые снова начинают размножаться.