	Уровень:

Задачи для самостоятельного решения по теме "неопределенный интеграл"

1. Решение.

На третьем шаге использовали формулу 14 и свойство 4 , где.

2. Решение.

Первый шаг - внесение под знак дифференциала функции : .

Второй шаг - внесение под знак дифференциала функции

Третий шаг - подынтегральную функцию записываем в виде степени с показателем и основанием

Далее используем формулу 1 , где и свойство 4 , где .

3. Решение. Первый шаг - внесение под знак дифференциала функции

Второй шаг - внесение под знак дифференциала функции :

Третий шаг - подынтегральную функцию записываем в виде степени с показателем и основанием .

Далее используем формулу 1 , где и свойство 4 , где .

4. Решение.

Первый шаг - внесение множителя под знак дифференциала

Второй шаг - внесение под знак дифференциала функции

Третий шаг - использование формулы 2 и свойства 4 , где .

5. Решение.

Первый шаг - внесение множителя под знак дифференциала:

Второй шаг - внесение функции под знак дифференциала

6. Решение.

Первый шаг - использована формула тригонометрии:

Второй шаг - вносим под знак дифференциала функцию :

Третий шаг - вносим под знак дифференциала функцию :

Четвертый шаг - использование формулы 13 , где и свойства 4 , где

7. Решение.

Разложим дробь на простейшие дроби: . Тогда .

Первый из этих интегралов возьмем по частям, положив , , откуда , и .

Второй интеграл берется подведением под знак дифференциала: .

Таким образом, 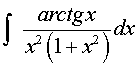= + +C.

8. Решение.

Сначала сделаем замену переменной , . Тогда = .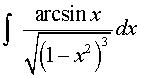

Последний интеграл возьмем по частям, полагая u = t , , откуда и

9. Решение.

Обозначим искомый интеграл через J. Положим , . Тогда , и =

В последнем интеграле снова положим , , таким образом и . Следовательно

= .

Решая это равенство, как уравнение относительно J, получим , тогда .

10. Решение.

Обозначим искомый интеграл через J. Положим , . Тогда , v = x и .

Преобразуем подынтегральное выражение: .

Тогда , откуда .

11. Решение. Обозначим = J.

Положим , , откуда. Тогда .

Здесь снова положим , , откуда .

Следовательно

12. Решение. Преобразуем подынтегральное выражение .

Тогда J = =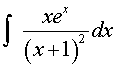

Второй интеграл возьмем по частям, полагая . Тогда