	Уровень:

Дифференциальное уравнение сохранения энергии

3.1 Закон сохранения энергии

Изучив явление теплопроводности, Фурье в 1822 году установил, что количество переносимого тепла в единицу времени через единицу площади q Дж/(м²с) Вт/м² пропорционально нормальной составляющей градиента температур grad_nt = dt/dn:

q = -

grad_nt.(3.1)

Это уравнение является математическим выражением основного закона распостранения тепла путем теплопроводности - закона Фурье. Множитель пропорциональности в (3.1) называют коэффициентом теплопроводности . Он характеризует способность вещества проводить тепло

,(3.1a)

Коэффициент теплопроводности изменяется в широких пределах от сотен до сотых долей единиц, то есть примерно на шесть порядков, например, теплопроводность серебра равна 450, а разреженного газа - несколько тысячных долей.

Если помимо теплопроводности перенос тепловой энергии сопровождается конвекцией, то переходим к обобщенному закону Фурье

(3.2)

Рассмотрим процесс переноса энергии вдоль координаты x в движущейся среде. На рис.3.1 показан перенос количества тепла Q (Дж) в сечениях x и x + x.

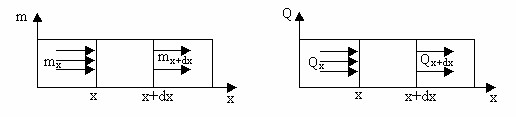
На основании закона сохранения энергии запишем, что разность между входящим в единичную площадку количеством тепла Q_x и идет на изменение его dQ в объеме dx*1, то есть

Q_x -

= dQ.

Введем понятие потока энергии, равного переносимому количеству энергии в единицу времени через единицу площади к нормали поверхности, то есть

q = Q/(

S) Дж/(м²с) = Вт/м² Выразим энергию Q через поток энергии q Q_x = q_xd

*1,

*1, а изменение тепловой энергии в объеме dx представим как dQ = c

xdt.
Подставим эти величины в уравнение (3.1) q_xd

*1 -

*1 = C

*1*

xdt и проведем следующие преобразования

.(3.3) В этом уравнении дано математическое выражение закона сохранения энергии.

3.2 Математическая модель закона переноса энергии

Для представления уравнения (3.3) с одной переменной t необходимо выразить зависимость теплового потока от температуры q = q(t). Такую зависимость дает закон Фурье для твердого тела (3.1) и обобщенный закон Фурье для движущейся среды (3.2). Подставляя значение потока (3.2) в уравнение (3.3), получим

, или

,(3.4)

Полагая = const и принимая во внимание зависимость = ac_V ,(3.5) получим

Аналогичные преобразования нетрудно провести для осей y и z, а затем записать полученные выражения и получить дифференциальное уравнение для трехмерной системы координат (x,y,z):

, или в векторной форме

(3.6)

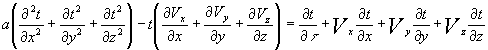По той же схеме можно вывести дифференциальное уравнение теплопроводности для тела с объемным источником тепла q_V (x,y,z, )

(3.7)

В самом общем случае можно учесть тепло, которое из-за внутреннего трения слоев жидкости друг об друга, и вызывающее повышение температуры в жидкости. Соответствующее дифференциальное уравнение примет вид:

,(3.8) где

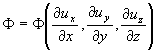так называемая диссипативная функция, вид которой здесь не приводим.