Дифференциальное уравнение импульсов
4.1 Вязкость ньютоновских и неньютоновских жидкостей
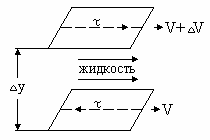
На рис.4.1 представлены две плоскости жидкости, отстоящие друг от друга на расстояние 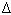 y, и движущиеся с разными скоростями V и V +
y, и движущиеся с разными скоростями V и V +  V. При
V. При 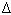 y
y  0 между слоями жидкости возникают касательные напряжения: это сила на единицу площади, которую надо приложить к плоскости, чтобы поддержать постоянную скорость.
0 между слоями жидкости возникают касательные напряжения: это сила на единицу площади, которую надо приложить к плоскости, чтобы поддержать постоянную скорость.
Согласно закону о трении Ньютона
 =
= 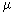 *
* V/
V/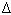 y, или
y, или  =
= 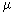 *dV/dy, (4.1) где коэффициент пропорциональности
*dV/dy, (4.1) где коэффициент пропорциональности 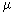 - динамическая вязкость жидкости, единица измерения которой равна
- динамическая вязкость жидкости, единица измерения которой равна
Н/м2 = 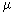 *м/(с*м), то есть [
*м/(с*м), то есть [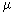 ] = Н*c/м2.
] = Н*c/м2. Кроме динамической вязкости жидкости употребляется так называемая кинематическая вязкость
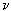 =
= 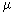 /
/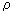 (4.2) [
(4.2) [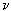 ] = м2/c.
] = м2/c. Для очень вязких жидкостей (вазелин, асфальт, нефть и другие) зависимость между касательным напряжением  и нормальной производной скорости
и нормальной производной скорости  V/
V/ y имеет более сложный вид
y имеет более сложный вид
 = k(
= k( V/
V/ y)n, (4.3) где n - эмпирический показатель степени.
y)n, (4.3) где n - эмпирический показатель степени. Жидкости, касательное напряжение которых описывается уравнением (4.3), называют ньютоновскими жидкостями.
4.2 Силы, действующие на объем движущейся жидкости
Определение. Движущейся объем dxdydz жидкости подчиняется второму закону Ньютона
Fx = Max = MVx/ = MdVx/d
= MdVx/d =
= 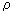 dxdydzdVx/d
dxdydzdVx/d , (4.4) где Fx - сила в направлении x, приложенная к объему жидкости массой M, Vx - скорость движения этого объема, ax - ускорение этого объема.
, (4.4) где Fx - сила в направлении x, приложенная к объему жидкости массой M, Vx - скорость движения этого объема, ax - ускорение этого объема.
Результирующая сила складывается из так называемой массовой силы dFxм и силы, вызывающей механическое напряжение на поверхности элемента dFнапр
dFx = dFxм + dFнапр.(4.5) Массовая сила действует на весь объем жидкости; она может быть вызвана гравитацией
dFxм = gcos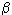 dxdydz = Xdxdydz,(4.6) где
dxdydz = Xdxdydz,(4.6) где 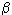 - угол между осью x и направляющей действия силы тяжести.
- угол между осью x и направляющей действия силы тяжести.
Рассмотрим механические напряжения, возникающие со стороны окружающей жидкости. На рис.4.2 представлен элемент жидкости, на каждой грани которого возникают механические напряжения, причем из-за разности скоростей плоскостей объема направление этих сил противоположно. Каждое из напряжений может быть разложено на три составляющие параллельные трем осям
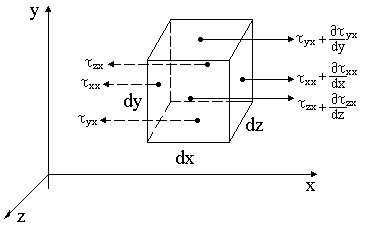 . Примем следующие обозначения:
. Примем следующие обозначения:
первый индекс - грань, на которую действует сила, указывает ось, перпендикулярную грани;
второй индекс - направление, в котором действует сила.
Смешанные индексы (xy) - касательные напряжения; одинаковые индексы (xx) - нормальные силы (напряжения).
Положительным направлением будем считать растягивающие нормальные напряжения. При стремлении элемента к нулю напряжения на противоположных гранях становятся равнымипо величине и противоположными по знаку. Например, на грань x действуют напряжения  xx,
xx,  xy,
xy, xz (рис.4.3).
xz (рис.4.3).
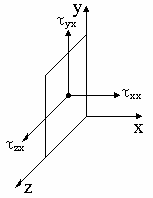
Поэтому напряженное состояние в точке характеризуется заданием шести касательных и трех нормальных напряжений, причем
 xy =
xy =  yx,
yx,  xz =
xz =  zx,
zx,  yz =
yz =  zy.(4.7) Давление связано нормальным напряжением соотношением - p = 1/3(
zy.(4.7) Давление связано нормальным напряжением соотношением - p = 1/3( xx +
xx +  yy +
yy +  zz). (4.8) Условились считать положительное давление для сжатия, а напряжения положительны при растяжении, этим вызван знак (-) в уравнении (4.8).
zz). (4.8) Условились считать положительное давление для сжатия, а напряжения положительны при растяжении, этим вызван знак (-) в уравнении (4.8). 4.3 Уравнение движения (импульсов) в напряжениях
Рассмотрим снова рис.4.1 и выпишем выражение для x-компоненты силы, которая вызывает изменение напряжения
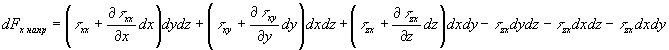 . К этой силе добавим массовую силу (4.6) и подставим в (4.5)
. К этой силе добавим массовую силу (4.6) и подставим в (4.5) 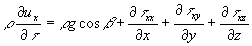 .(4.9) По аналогии запишем подобные выражения для других осей
.(4.9) По аналогии запишем подобные выражения для других осей 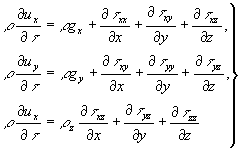 .(4.10) Уравнения (4.10) связывают скорости Vi с напряжениями
.(4.10) Уравнения (4.10) связывают скорости Vi с напряжениями  ij и носят название уравнений движения в напряжениях.
ij и носят название уравнений движения в напряжениях.
4.4 Связь напряжений с вязкостью
Известно, что упругие тела деформируются в соответствии с законом Гука (напряжение пропорционально деформации), но для жидкостей напряжение пропорционально скорости деформации
 =
= 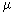 (dvx/dy).(4.11) При более сложных деформациях скорость деформации удобно определять как скорость изменения угла
(dvx/dy).(4.11) При более сложных деформациях скорость деформации удобно определять как скорость изменения угла 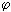 , показанного на рис.4.4.
, показанного на рис.4.4. 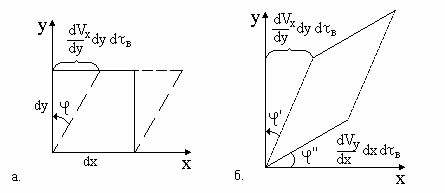 ,
, Для одномерного слуая изменение угла 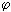 (в радианах) за время d
(в радианах) за время d есть d
есть d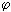 , и его можно выразить как величину дуги dVx/dy, деленную на радиус dy, то есть
, и его можно выразить как величину дуги dVx/dy, деленную на радиус dy, то есть
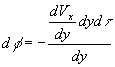 , поэтому скорость деформации d
, поэтому скорость деформации d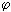 /d
/d = - dVx/dy.(4.12) Подставим (4.12) в (4.11) и полуим следующее выражение для
= - dVx/dy.(4.12) Подставим (4.12) в (4.11) и полуим следующее выражение для  xy:
xy:  xy =
xy = 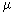 d
d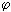 / d
/ d . (4.13)
. (4.13) Рассмотрим теперь деформацию элемента (рис.4.:) и используем уравнение (4.13). На рисунке показана деформация, которую вызывают напряжения, действующие на гранях, перпендикулярных плоскости xy. Видно, что изменения угла 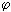 складываются из двух частей: первая равна (-
складываются из двух частей: первая равна (-  Vx /
Vx / y) d
y) d , а вторая - (
, а вторая - ( Vy/
Vy/ x)dy, получаем
x)dy, получаем

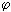 /
/ 
 = - (
= - ( Vx/
Vx/ y +
y +  Vy/
Vy/ x). Подставим это значение
x). Подставим это значение 
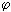 /
/ 
 в уравнение (4.13)
в уравнение (4.13)  xy =
xy =  yx =
yx = 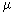 ((
(( Vx/
Vx/  y +
y + Vy/
Vy/ x)).(4.14)
Аналогично получим другие касательные напряжения
x)).(4.14)
Аналогично получим другие касательные напряжения  xz =
xz =  zx =
zx = 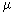 ((
(( Vx/
Vx/  z +
z + Vz/
Vz/ x)),
x)),  yz =
yz =  zy =
zy = 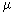 ((
(( Vy/
Vy/  z +
z + Vz/
Vz/  y)).(4.15)
y)).(4.15) 4.5 Нормальные напряжения
По определению (4.8) имеем
- p = 1/3( xx +
xx +  yy +
yy +  zz). Представим нормальное напряжение как бы состоящим из двух частей: первая часть обусловлена давлением, вторая - деформацией элемента жидкости в этом направлении
zz). Представим нормальное напряжение как бы состоящим из двух частей: первая часть обусловлена давлением, вторая - деформацией элемента жидкости в этом направлении
 xx = -p +
xx = -p + 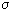 x. (4.16) Велиина p определена уравнением (4.8), используем его совместно с уравнением (4.16)
x. (4.16) Велиина p определена уравнением (4.8), используем его совместно с уравнением (4.16)
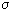 x =
x =  xx + p;
xx + p;  xx =
xx =  xx - 1/3(
xx - 1/3( xx +
xx +  yy +
yy +  zz); откуда
zz); откуда 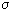 x = 2/3
x = 2/3 xx - 1/3(
xx - 1/3( yy +
yy +  zz); Удобно разделить
zz); Удобно разделить 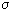 x на две части
x на две части 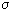 x = 1/3(
x = 1/3( xx +
xx +  yy)+ 1/3(
yy)+ 1/3( xx +
xx +  zz). Аналогично введем уравнения для
zz). Аналогично введем уравнения для 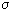 y и
y и 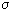 z, затем подставим выражения для
z, затем подставим выражения для 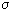 i в уравнение (4.16) и получим
i в уравнение (4.16) и получим 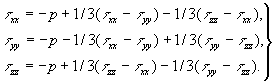 .(4.17) Дальнейшие выкладки довольно громоздки, но после всех преобразований, которые приведены в [:], получим следующие выражения для нормальных напряжений
.(4.17) Дальнейшие выкладки довольно громоздки, но после всех преобразований, которые приведены в [:], получим следующие выражения для нормальных напряжений 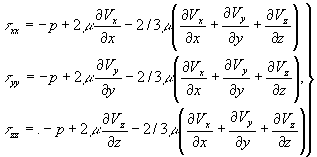 (4.18)
(4.18)
4.6 Уравнение Навье-Стокса или уравнение движения
Подставим уравнения (4.14), (4.15) и (4.18) в уравнение (4.10); тогда получим после преобразований уравнение движения
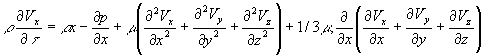 (4.19) Аналогично можно записать уравнения для осей y, z. Эти уравнения называются уравнениями Навье-Стокса или движения. В дальнейшем в основном будет рассматриваться несжимаемая жидкость, для которой справедливо уравнение неразрывновсти
(4.19) Аналогично можно записать уравнения для осей y, z. Эти уравнения называются уравнениями Навье-Стокса или движения. В дальнейшем в основном будет рассматриваться несжимаемая жидкость, для которой справедливо уравнение неразрывновсти 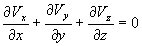 и уравнение Навье-Стокса принимает более простой вид
и уравнение Навье-Стокса принимает более простой вид 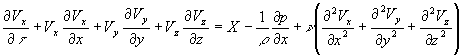 (4.20) Аналогично будут выглядеть уравнения для осей y и z. Многие технические задачи могут быть упрощены (например, несжимаемые жидкости, одномерные задачи и так далее). Запишем выражение (4.19) в векторной форме
(4.20) Аналогично будут выглядеть уравнения для осей y и z. Многие технические задачи могут быть упрощены (например, несжимаемые жидкости, одномерные задачи и так далее). Запишем выражение (4.19) в векторной форме 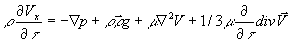 (4.21) Если вязкость мала
(4.21) Если вязкость мала 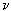 =0 и жидкость несжимаема, то уравнение существенно упрощается, так как
=0 и жидкость несжимаема, то уравнение существенно упрощается, так как 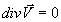 и
и 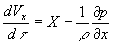 (4.22) Это уравнение было полученло Эйлером и носит его имя.
(4.22) Это уравнение было полученло Эйлером и носит его имя.








![]() y, и движущиеся с разными скоростями V и V +
y, и движущиеся с разными скоростями V и V + ![]() V. При
V. При ![]() y
y ![]() 0 между слоями жидкости возникают касательные напряжения: это сила на единицу площади, которую надо приложить к плоскости, чтобы поддержать постоянную скорость.
0 между слоями жидкости возникают касательные напряжения: это сила на единицу площади, которую надо приложить к плоскости, чтобы поддержать постоянную скорость.
![]() и нормальной производной скорости
и нормальной производной скорости ![]() V/
V/![]() y имеет более сложный вид
y имеет более сложный вид  .
.
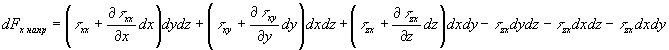 .
.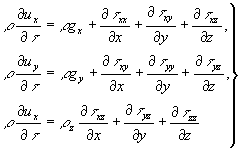 .(4.10)
.(4.10) ,
,![]() (в радианах) за время d
(в радианах) за время d![]() есть d
есть d![]() , и его можно выразить как величину дуги dVx/dy, деленную на радиус dy, то есть
, и его можно выразить как величину дуги dVx/dy, деленную на радиус dy, то есть 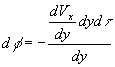 ,
,![]() складываются из двух частей: первая равна (-
складываются из двух частей: первая равна (- ![]() Vx /
Vx /![]() y) d
y) d![]() , а вторая - (
, а вторая - (![]() Vy/
Vy/![]() x)dy, получаем
x)dy, получаем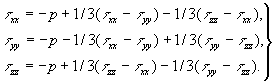 .(4.17)
.(4.17)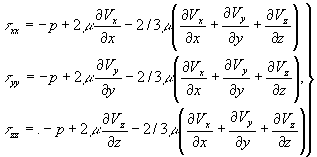 (4.18)
(4.18)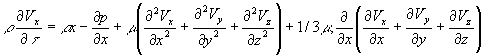 (4.19)
(4.19)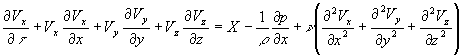 (4.20)
(4.20)