







|
|
|
|
|
||
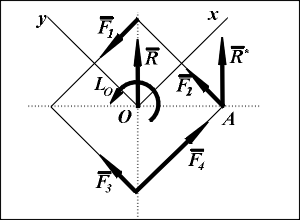
Пример. К вершинам квадрата со стороной a = 0.5(м) приложены силы: F1 = F2 = F3 = 2(Н); F4 = 6(Н). Определить равнодействующую этой системы сил.
Решение. Введем координатную систему Oxy с началом координат в центре квадрата О и осями Ox,Oy, параллельными сторонам квадрата. Приведем данную систему сил к центру О, вычислив проекции главного вектора R и алгебраический главный момент LO относительно точки О:
Rх = F1x + F2x + F3x + F4x = -F1 + 0 + 0 + F4= -2 + 6 = 4(Н);
Ry = F1y + F2y + F3y + F4y = 0 + F2 + F3 + 0 = 2 + 2 = 4(Н);
LO = F1·a/2 + F2·a/2 - F3·a/2 + F4·a/2 = 0.5 + 0.5 - 0.5 + 1.5 = 2(Н·м).
Главный вектор R имеет модуль R=(R2x + R2y)![]() =4
=4![]() (Н) и направлен по диагонали квадрата. Для построения равнодействующей силы R* вектор R необходимо параллельно перенести на расстояние OA = LO/R = 0.25
(Н) и направлен по диагонали квадрата. Для построения равнодействующей силы R* вектор R необходимо параллельно перенести на расстояние OA = LO/R = 0.25![]() (м), равное половине длины диагонали квадрата.
(м), равное половине длины диагонали квадрата.
Таким образом, равнодействующей силой данной системы сил является вектор R*, равный по модулю 4![]()
![]() 5.64(Н), приложенный к вершине квадрата А и направленный перпендикуляно отрезку ОА.
5.64(Н), приложенный к вершине квадрата А и направленный перпендикуляно отрезку ОА.
Замечание. Для определения равнодействующей приведение заданной системы сил можно выполнять к произвольно выбранному центру О. Целесообразно использовать такой центр О и координатные оси Ox,Oy, для которых вычисления главного вектора R и алгебраического главного момента LO проводятся наиболее простым образом.