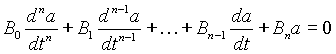
Все процессы в электрических цепях можно рассматривать в двух режимах - установившемся и переходном.
Установившимся режимом называют такое состояние электрической цепи, когда параметры ее элементов, токов и напряжений остаются неизменными. Переходным режимом или переходным процессом в электрической цепи называют режим, при котором параметры элементов или параметры токов и напряжений изменяются в функции времени.Изменение параметров электрической цепи может происходить только за конечный промежуток времени, т.к. оно связано с изменением количества энергии, запасенной в электрических и магнитных полях. Однако при анализе переходных процессов обычно пренебрегают существованием электрических или магнитных полей на том или ином участке цепи, считая что ток или напряжение мгновенно изменяются на некоторую конечную величину.
Процесс скачкообразного (мгновенного) изменения какого-либо параметра электрической цепи называется коммутацией. При анализе переходных процессов отсчет времени принято производить от этого момента.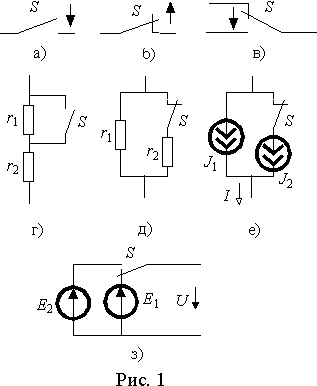
Обычно процесс коммутации на электрической схеме изображается идеальным ключевым элементом. Идеальный ключ S
Коммутация любой степени сложности может быть осуществлена тремя типами ключей - замыкающими, размыкающими и переключающими (рис. 1 а), б), и в)). Условное обозначение ключей является интуитивно понятной стилизацией механического переключателя. Иногда рядом с ключами стрелкой показывают движение подвижной части при коммутации.
На рис. 1 г) и д) показаны примеры реализации с помощью ключей мгновенного изменения сопротивления. В первом случае значение сопротивления при коммутации изменяется от
r1+r2 до r2, а во втором - от r1r2/( r1+r2) до r1. Аналогично с помощью ключей можно скачкообразно изменять ток и напряжение источников. На рис. 1 е) ток I скачком изменяется от J1+J2 до J1, а на рис. 1 з) напряжение U при коммутации изменяется от E1 до E2 .Как уже отмечалось выше, наличие электрических и магнитных полей не позволяет произвести мгновенное изменение состояния цепи. Поля на электрических схемах обозначаются индуктивностями и емкостями. При этом напряжение на индуктивности цепи равно
uL = LЧ diL/dt, а ток через емкость - iC = CЧ duC/dt. Таким образом, мгновенное изменение тока в индуктивности iL или напряжения на емкости uC должны создавать бесконечно большое напряжение или ток на соответствующем участке цепи, нарушающие законы Кирхгофа. Но законы Кирхгофа не могут нарушаться в принципе, т.к. они являются одной из форм закона сохранения энергии. Следовательно, скачкообразное изменение рассмотренных параметров невозможно, что формулируется в виде законов коммутации:В теории переходных процессов под
i(0- ) понимают значение некоторой величины в момент времени непосредственно предшествующий коммутации, а под i(0+) - значение этой величины в момент времени непосредственно следующий за коммутацией.В простейшем случае переходному процессу предшествует установившийся режим и заканчивается он также установившимся режимом.
Значения токов и напряжений в электрической цепи в момент времени t = 0 называются начальными значениями или начальными условиями. Причем эти значения при коммутации могут изменяться или оставаться постоянными в первый момент времени. Начальные значения, не изменяющиеся при коммутации и определяемые по состоянию цепи до нее, называются независимыми начальными значениями. Очевидно, к ним относятся токи в индуктивностях и напряжения на емкостях. Остальные начальные значения величин называются зависимыми и определяются по состоянию цепи после коммутации с учетом независимых начальных значений.Значения токов и напряжений в цепи
после переходного процесса, т.е. при t = µ , называются установившимися значениями.Начальные и установившиеся значения величин можно определить с помощью любых методов расчета электрических цепей в установившемся режиме, например, с помощью уравнений Кирхгофа.
Как известно, напряжения и токи в индуктивностях и емкостях являются производными и интегралами соответствующих величин. Поэтому уравнения Кирхгофа для электрической цепи содержащей реактивные элементы будут дифференциальными или интегро-дифференциальными и задачей анализа переходных процессов является их решение
.Для несложных электрических цепей с постоянными параметрами систему уравнений Кирхгофа методом подстановки можно свести к одному дифференциальному уравнению с постоянными коэффициентами, порядок которого будет равен числу реактивных элементом цепи. Если в схеме цепи после коммутации отсутствуют источники электрической энергии, то уравнение будет однородным, т.е. его правая часть будет равна нулю, в противном случае уравнение будет неоднородным.
Из курса математики известно, что решение неоднородного дифференциального уравнения можно представить в виде суммы общего решения однородного уравнения и какого-либо частного решения неоднородного. Решение однородного дифференциального уравнения соответствует процессам в электрической цепи при отсутствии внешних источников энергии, т.е. режиму, при котором энергия электрических и магнитных полей преобразуется без внешнего воздействия. Эта составляющая решения называется свободной составляющей
.Свободную составляющую решения ищут в виде функции
a=Aept . Эта функция замечательна тем, что n-я производная от нее равна pnAept. Поэтому при подстановке ее в однородное дифференциальное уравнение n-го порядка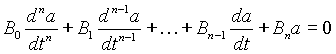
получим
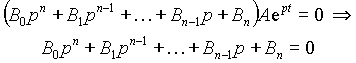
Последнее выражение называется характеристическим уравнением. Корни характеристического уравнения определяют показатели экспонент решения однородного дифференциального уравнения. Из приведенных преобразований следует, что характеристическое уравнение можно получить из дифференциального формальной заменой производной
k-го порядка на pk.Частное решение неоднородного дифференциального уравнения обычно проще найти для установившегося режима и его называют установившейся составляющей
.Определение составляющих решения дифференциального уравнения не является обязательным, если анализ переходных процессов выполняется операторным методом, т.к. в этом случае полное решение получается в процессе перехода от изображения к оригиналу.
В анализе переходных процессов особую роль играет показательная функция вида
a(t) = Ae-t/t , где e - основание натуральных логарифмов, или экспонента. Это связано с тем, что решения дифференциальных уравнений представляют собой сумму экспонент.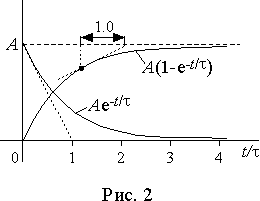
Экспонента обладает рядом особенностей, которые имеют большое значение при анализе переходных процессов. Значение e
-t/t при t = 0 равно единице, поэтому a(0) = A. При t ® µ , e-t/t ® 0 и a(t) ® 0Коэффициент
t , имеющий размерность времени, определяет скорость изменения величины a(t) и называется постоянной времени экспоненты. Чем меньше постоянная времени, тем быстрее протекает переходный процесс. Выберем произвольно два момента времени, отстоящие друг от друга на время t . Значения a(t) для этих моментов - a1(t) = Ae-t/t и a2(t) = Ae-(t+t)/t , а их отношение a1(t)/a2(t) = e-(t- t-t )/t = e, следовательно, в течение постоянной времени величина a(t) изменяется в е-раз. Графически это свойство экспоненты проявляется в том, что касательная к ней в любой точке пересекает установившееся значение в точке, отстоящей по времени от точки каcания на величину t (рис. 2).Теоретически экспонента в течение конечного интервала времени не достигает установившегося значения, т.е. любой переходный процесс должен продолжаться бесконечно. Однако при
t = 3t значение экспоненты отличается от установившегося на 5%. Поэтому интервал времени равный 3t считают длительностью переходного процесса.В анализе переходных процессов столь же часто как функция
a(t) = Ae-t/t встречается функция a(t) = A(1- e-t/t) (рис. 2). Она обладает теми же свойствами и отличается только установившимся значением.