3.2. Задача Дирихле для уравнения Лапласа в круге
Найти функцию U, удовлетворяющую уравнению:
внутри круга |
(1) |
и граничному условию
на границе круга, |
(2) |
где 
-заданная
функция, 
-полярный
угол.
.
Введем полярную систему координат 
с началом в центре круга.
-полярные
координаты.
Уравнение (1) в полярных координатах имеет вид
 . |
(3) |
Решим уравнение методом разделения переменных, то есть будем искать частное решение уравнения (1), вида
.
Подставляя предполагаемую форму решения в уравнение (3), получим
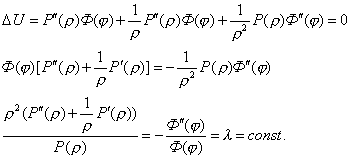
Отсюда получим два обыкновенных дифференциальных уравнения:
 |
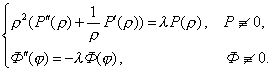(4) (5) |
Определим знак 
:
1 случай Пусть
например
Рассмотрим уравнение (5)
Характеристическое уравнение имеет вид
-это
решение не подходит, так как при изменении угла
на величину 
однозначная функция 
должна вернуться к исходному значению 
(условие периодичности).
Отсюда следует, что 
то
есть 
является
периодической функцией
угла
с периодом .
2 случай Пусть
,
тогда
-это
решение подходит для уравнения (5) системы при условии, что A=0.
Рассмотрим уравнение (4) системы:
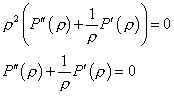
Пусть 
тогда:
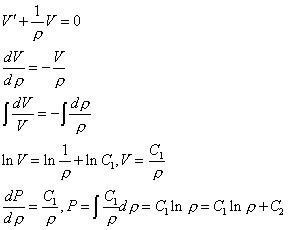
Таким образом получаем : 
-решение
уравнения в общем случае.
3 случай Пусть
например 
Решение уравнения (5):
причем 
.
Рассмотрим уравнение (4) системы:
Функцию 
будем искать в виде 
Подставим 
в уравнение (4):
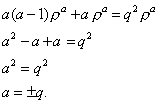
Следовательно, 
-
решение уравнения, где C и D
–постоянные.
Для решения внутренней задачи надо положить
,
так как, если 
,
то
функция 
обращается в бесконечность при 
и не является
гармонической функцией внутри круга. Итак, частные решения нашей задачи найдены:
,
 -вид
общего решения. |
(6) |
Удовлетворим краевому условию:
Считая, что 
задана как функция угла ,
возьмем ее разложение в ряд Фурье
где
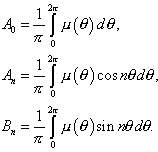
Подставляя выражения для коэффициентов Фурье в формулу (6) и меняя порядок суммирования и интегрирования, получим
 |
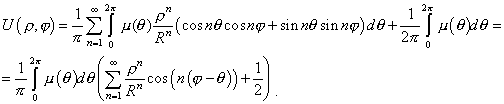(8) |
Произведем следующие тождественные преобразования:
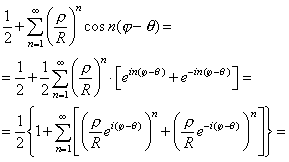
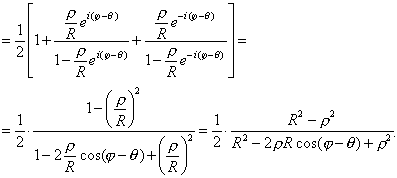
Подставляя полученный результат в равенство (8), получаем
-интегральная
формула, дающая решение задачи.
-ядро
Дирихле.