2.1. Метод разделения переменных для конечного стержня.

2. Уравнение теплопроводности

2.1. Метод разделения переменных для конечного стержня

Уравнение теплопроводности относится к уравнениям параболического типа.

Уравнение теплопроводности имеет вид:

,
- температура стержня в точке в момент времени ,
- связано с коэффициентами теплоемкости и теплопроводности.

Рассмотрим однородный стержень длины , теплоизолированный с боков и достаточно тонкий, чтобы в любой момент времени температуру во всех точках поперечного сечения можно было считать одинаковой (см. рисунок 1).

Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия. Для задач этого типа задается только одно начальное условие, а именно, начальная температура в начальный момент времени. Итак,

. (1)

Краевые условия:

,
(2)

(3)

где -начальное распределение температуры в стержне.

Концы стержня закреплены в термостате. В данном случае тепловая энергя стержня не сохраняется, так как система не является изолированной.
Будем искать решение в виде произведения двух функций

где X(x)- функция только переменного x,
а T(t)- функция только переменного t.

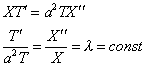
, так как левая часть равенства зависит только от t, а правая – только от x. Отсюда следует, что

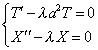
Граничные условия (3) дают:
X(0)=0 , X()=0,
тогда

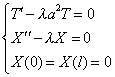(4)

(5)

(6)

Необходимо определить знак .

1 случай: Пусть .
Рассмотрим уравнение (4):
.
Характеристическое уравнение имеет вид:
.

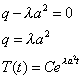Рассмотрим уравнение (5):
.
Характеристическое уравнение имеет вид:

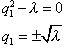
. (7)

Это решение не подходит, так как если ,то , а поэтому нарушается второй закон термодинамики, то есть происходит передача энергии от холодного к горячему. Докажем это математически, подставив начальные условия (6) в (7):

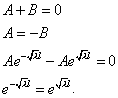
Значит или , но тогда мы получаем тривиальное решение и не можем удовлетворить начальным условиям. Следовательно, при уравнение (1) имеет только нулевое решение.
2 случай: Пусть , тогда
, следовательно,.
, следовательно, .
Подставим краевые условия
, получим .
В итоге получим нулевое решение , а значит не подходит.

3 случай: Пусть и , тогда
.
Характеристическое уравнение имеет вид:

Общее решение может быть записано в виде:

. (8)

Подставим краевые условия.
.
Получаем

. (9)

Существуют нетривиальные решения уравнения (5), равные

. (10)

Этим значениям соответствуют решения уравнения (4)
,
где - неопределенный пока коэффициент.

- общее решение.

Удовлетворим начальным условиям (2):
.
Для выполнения этого начального условия необходимо взять в качестве коэффициент Фурье:

.
Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.

<<назад главная страница вперед>>