1.4. Метод Фурье

1.4. Метод Фурье (метод стоячих волн, метод разделения переменных)
1.4.1. Метод разделения переменных для струны, закрепленной на концах
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах.
Итак, будем искать решение уравнения

,
(1)

удовлетворяющее однородным граничным условиям

U(0, t) = U(l, t) = 0 (2)

и начальным условиям

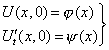. (3)

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Будем искать решение уравнения в виде

, (4)

где X(x)- функция только переменного ,

T(t)- функция только переменного .

Подставим (4) в уравнение (1), получим:

. (5)

Чтобы функция (4) была решением уравнения (1), равенство (5) должно удовлетворяться тождественно, то есть для всех значений независимых переменных , . Правая часть равенства (5) является функцией только переменного x, а левая- только .

Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части (5) при изменении своих аргументов сохраняют постоянное значение, то есть

. (6)

Из соотношения (6) получаем обыкновенные дифференциальные уравнения для определения функций X(x) и T(t) .

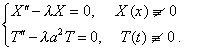(7)

(8)

Граничные условия (2) дают:

.

Отсюда следует, что функция X(x) должна удовлетворять дополнительным условиям

X(0) =X(l) =0, (9)

так как иначе мы имели бы T(t)≡0 и U(x, t)≡0, в то время как задача состоит в нахождении нетривиального решения.

Таким образом, в связи с нахождением функции X(x) мы приходим к простейшей задаче о собственных значениях: найти такие значения параметра λ, при которых существуют нетривиальные решения задачи:

(10)

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (10).
Итак, найдем знак :

1 случай , например, .
Запишем характеристическое уравнение для (10):

.
Общее решение уравнения может быть записано в виде
.
Граничные условия дают:
,
то есть и .
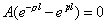Но в рассмотренном случае - действительно и положительно, так что .
Поэтому , и, следовательно, , а мы ищем нетривиальное решение.
2 случай Пусть .

При также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (7) имеет вид
.
Граничные условия дают:

то есть A=0 и B=0 и, следовательно, .

3 случай , например .
Характеристическое уравнение имеет вид

.

Общее решение уравнения:
.

Граничные условия дают:
.
Если , то . Поэтому

, где n- любое целое число. Обозначим p через ,
.

- нетривиальное решение задачи (10), (11)

определяемое с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям соответствуют решения уравнения (8).

, (12)

где и - произвольные постоянные.

Возвращаясь к задаче (1) – (3), заключаем, что функции
являются частными решениями уравнения (1), удовлетворяющими граничным условиям (3) и представимыми в виде произведения (4) двух функций.
Обратимся к решению в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений

(13)

также удовлетворяет этому уравнению и граничным условиям (2).

Начальные условия позволяют определить и . Потребуем, чтобы функция (13) удовлетворяла условиям (3):

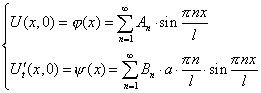. (14)

Если функции и удовлетворяют условиям разложения в ряд Фурье, то

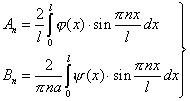. (15)

Подставив (15) в (13), мы удовлетворим краевым условиям и получим решение уравнения.

<<назад главная страница вперед>>